Question

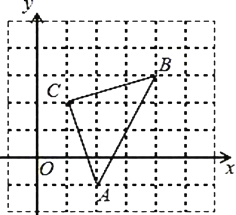
【题目】如图，点的坐标为，作轴，轴，垂足分别为，，点为线段的中点，点从点出发，在线段、上沿运动，当时，点的坐标为________．

Answer 1

【答案】（2，4）或（4，2）

【解析】

根据点B的坐标和已知条件可得AO=OC=AB=BC=4，∠OAB =∠COD =∠OCB=90°，OD=2，然后根据点P的位置分类讨论，分别画出对应的图形，根据全等三角形的判定及性质即可求出结论．

解：∵点的坐标为，轴，轴，点为线段的中点，

∴AO=OC=AB=BC=4，∠OAB =∠COD =∠OCB=90°，OD=2

①当点P在AB上时，如下图所示

在Rt△OAP和Rt△COD中

∴Rt△OAP≌Rt△COD

∴AP=OD=2

∴点P的坐标为（4,2）；

②当点P在BC上时，如下图所示

在Rt△OCP和Rt△COD中

∴Rt△OCP≌Rt△COD

∴CP=OD=2

∴点P的坐标为（2,4）；

综上：点P的坐标为（2,4）或（4,2）

故答案为：（2,4）或（4,2）．