练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小明将一根长为20厘米的铁丝剪成两段，然后分别围成两个正方形。设其中一段铁丝长为x厘米。

    （1）设较长的一段铁丝长为xcm，请计算出这两个正方形的面积之差；
    （2）是否存在合适的x的值，使两个正方形的面积刚好相差5cm2？请说明理由.

    【答案】（1）x-25；（2）即当x=12时，这两个正方形的面积刚好相差5cm2．

    【解析】

    （1）根据正方形的周长公式得到其边长，然后计算其面积即可；
    （2）假设存在这样的x值，根据面积相差5cm2，列出关于x的方程，然后解方程．

    （1）依题意得，x-25．
    即这两个正方形的面积之差为：x-25．
    （2）假设存在这样的x值，使两个正方形的面积刚好相差5cm2．则
    x-25=5，
    解得x=12．符合题意．
    即当x=12时，这两个正方形的面积刚好相差5cm2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③.

    (1)图②有______个三角形；图③有______个三角形；

    (2)按上面的方法继续下去，第n个图形中有_________个三角形(用n的代数式表示).

    (3)是否存在正整数n，使得第n个图形中存在2019个三角形?如果存在，请求出n的值；如果不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数y= 的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（　　）

    A. y1＜y2＜y3B. y2＜y3＜y1C. y3＜y2＜y1D. y2＜y1＜y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

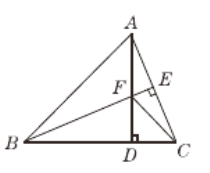
    【题目】如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF.

    （1）求证△ACD≌△BFD

    （2）求证：BF＝2AE；

    （3）若CD＝，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l1的函数解析式为y=﹣2x+4，且l1与x轴交于点D，直线l2经过点A、B，直线l1、l2交于点C．

    （1）求直线l2的函数解析式；

    （2）求△ADC的面积；

    （3）在直线l2上是否存在点P，使得△ADP面积是△ADC面积的2倍？如果存在，请求出P坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了备战初三物理、化学实验操作考试，某校对初三学生进行了模拟训练，物理、化学各有4个不同的操作实验题目，物理用番号①、②、③、④代表，化学用字母a、b、c、d表示，测试时每名学生每科只操作一个实验，实验的题目由学生抽签确定，第一次抽签确定物理实验题目，第二次抽签确定化学实验题目．

    （1）请用树形图法或列表法，表示某个同学抽签的各种可能情况．

    （2）小张同学对物理的①、②和化学的b、c号实验准备得较好，他同时抽到两科都准备的较好的实验题目的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A（2,0），B（6,0），CB⊥x轴于点B，连接AC

    画图操作：

    （1）在y正半轴上求作点P，使得∠APB=∠ACB（尺规作图，保留作图痕迹）

    理解应用：

    （2）在（1）的条件下，

    ①若tan∠APB ，求点P的坐标

    ②当点P的坐标为 时，∠APB最大

    拓展延伸：

    （3）若在直线yx+4上存在点P，使得∠APB最大，求点P的坐标

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，直至得C17.

    （1）写出点的坐标________

    （2）若P（50，m）在第17段抛物线C17上，则m=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解上一次八年级数学测验成绩情况，随机抽取了40名学生的成绩进行统计分析，这40名学生的成绩数据如下：

    55 62 67 53 58 83 87 64 68 85

    60 94 81 98 51 83 78 77 66 71

    91 72 63 75 88 73 52 71 79 63

    74 67 78 61 97 76 72 77 79 71

    （1）将样本数据适当分组，制作频数分布表：

    分 组

    　 　

    　 　

    　 　

    　 　

    　 　

    频 数

    　 　

    　 　

    　 　

    　 　

    　 　

    （2）根据频数分布表，绘制频数直方图：

    （3）从图可以看出，这40名学生的成绩都分布在什么范围内？分数在哪个范围的人数最多？

    查看答案和解析>>

    同步练习册答案