
【题目】如图,点A(﹣2,0)、B(4,0)、C(3,3)在抛物线y=ax2+bx+c上,点D在y轴上,且DC⊥BC,∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F.
(1)求抛物线的解析式;
(2)CF能否经过抛物线的顶点?若能,求出此时点E的坐标;若不能,说明理由;
(3)若△FDC是等腰三角形,求点F的坐标.
【答案】
(1)
解:由抛物线与X轴的两个交点A、B的坐标,
可以由两根式设抛物线解析式为:y=a(x+2)(x﹣4),
然后将C点坐标代入得:a(3+2)(3﹣4)=3,
解得:a=﹣ ![]() ,
,
故抛物线解析式是:y=﹣ ![]() (x+2)(x﹣4)
(x+2)(x﹣4)

(2)
解:由C、B两点坐标利用待定系数法可以求得CB直线方程为:y=﹣3x+12,
∵CD⊥CB,
∴CD直线方程可以设为:
y= ![]() x+m,
x+m,
将C点坐标代入得:m=2,
∴CD直线方程为:y= ![]() x+2,
x+2,
∴D点坐标为:D(0,2),
由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标为M(1, ![]() ),
),
∴由C、M两点坐标可以求得CM即CF直线方程为:y=﹣ ![]() x+
x+ ![]() ,
,
∴F点坐标为:F(0, ![]() ),
),
∴CE直线方程可以设为:y= ![]() x+n,
x+n,
将C点坐标代入得:n= ![]() ,
,
∴CE直线方程为:y= ![]() x+
x+ ![]() ,
,
令y=0,解得:x=﹣ ![]() ,
,
∴E点坐标为E(﹣ ![]() ,0),
,0),
∴能;
(3)
解:由C、D两点坐标可以求得CD= ![]() ,
,
则△FDC是等腰△可以有三种情形:
① FD=CD= ![]() ,
,
则F点坐标为F(0,2+ ![]() ),
),
②FC=CD= ![]() ,过C点作y轴垂线,垂足为H点,
,过C点作y轴垂线,垂足为H点,
则DH=1,
则FH=1,
则F点坐标为F(0,4),
③FD=FC,作DC的中垂线FG,交y轴于F点,交DC于G点,
由中点公式得G点坐标为G( ![]() ,
, ![]() ),
),
由DC两点可以求得DC直线方程为:y= ![]() x+2,
x+2,
则FG直线方程可以设为:y=﹣3x+p,
将G点坐标代入解得:p=7,
故F点坐标为(0,7).
【解析】(1)由抛物线与X轴的两个交点A、B的坐标,可以由两根式设抛物线解析式为:y=a(x+2)(x﹣4),求出a的值即可;(2)由C、B两点坐标利用待定系数法可以求得CB直线方程为:y=﹣3x+12,设CD直线方程可以设为:y= ![]() x+m,求出m的值,进而求出D点的值,由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标,由C、M两点坐标可以求得CM即CF直线方程,CE直线方程可以设为:y=
x+m,求出m的值,进而求出D点的值,由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标,由C、M两点坐标可以求得CM即CF直线方程,CE直线方程可以设为:y= ![]() x+n,求出n的值,进而求出E点的坐标;(3)由C、D两点坐标可以求得CD=
x+n,求出n的值,进而求出E点的坐标;(3)由C、D两点坐标可以求得CD= ![]() ,△FDC是等腰△可以有三种情形:①当FD=CD;②FC=CD;③FD=FC,分别求出F点的坐标即可;
,△FDC是等腰△可以有三种情形:①当FD=CD;②FC=CD;③FD=FC,分别求出F点的坐标即可;


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】某中学积极开展“阳光体育”活动,共开设了跳绳、乒乓球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)根据统计的数据估计该中学3200名学生中最喜爱篮球的人数约有_____人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,购进 4 件甲种商品比购进 5 件乙种商品少用 10 元,购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
(1)求甲、乙两种商品每件进价分别是多少元?
(2)若该商店购进甲、乙两种商品共 140 件,都标价 10 元出售,售出一部分降价促销, 以标价的八折售完所有剩余商品,以 10 元售出的商品件数比购进甲种商品件数少 20 件,该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元,求至少购进甲种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你写出勾股定理内容(用文字语言表述):
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以(a+b)为高的直角梯形(如图2),请你利用图2,证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
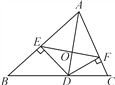
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE. 
(1)求证:BN=AN;
(2)猜想线段CD与DE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com