
 如图,AD是△ABC的边BC上的高,DE⊥AB,DF⊥AC,由下列条件中的某一个就能推出△ABC是等腰三角形的是①或②或③或④.(把所有正确答案的序号都填写在横线上)
如图,AD是△ABC的边BC上的高,DE⊥AB,DF⊥AC,由下列条件中的某一个就能推出△ABC是等腰三角形的是①或②或③或④.(把所有正确答案的序号都填写在横线上)分析 四个条件都可以推出△ABC是等腰三角形,根据等腰三角形的定义,一一证明即可.
解答 解:①当BD=CD时,∵AD⊥BC,
∴AB=AC,
∴△ABC是等腰三角形.
②当∠BAD=∠CAD时,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.
③当AB+BD=AC+CD时,延长DB至M,使BM=AB;延长DC至N,使CN=AC;连接AM、AN;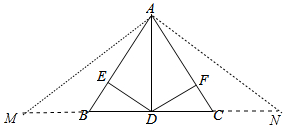
∵AB+BD=CD+AC,
∴DM=DN,又AD⊥BC;
∴△AMN是等腰三角形;
∴∠M=∠N;
∵AB=BE,
∴∠ABC=2∠M;
同理,得∠ACB=2∠N;
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
④当DE=DF时,∵DE⊥AB,DF⊥AC,
∴∠BAD=∠BAC,
由②可知,△ABC是等腰三角形.
故答案为①或②或③或④.
点评 本题考查等腰三角形的判定和性质、全等三角形的判定和性质、角平分线的判定定理等知识,解题的关键是灵活运用所学知识,学会添加辅助线,构造等腰三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
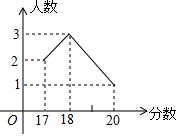 某校6名学生的某次竞赛成绩统计如图,则这组数据的众数、中位数、方差依次是( )
某校6名学生的某次竞赛成绩统计如图,则这组数据的众数、中位数、方差依次是( )| A. | 18,17.5,5 | B. | 18,17.5,3 | C. | 18,18,3 | D. | 18,18,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
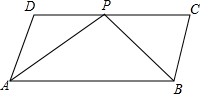 如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
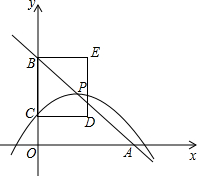 如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B,抛物线y=-$\frac{1}{3}$(x-m)2+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B,抛物线y=-$\frac{1}{3}$(x-m)2+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com