练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知y=mxm2+3m+2是二次函数，则m的值为（　　）
    A．0或-3B．0或3C．0D．-3
    依题意有：
    m2+3m+2=2，且m≠0，
    解得m=-3．
    故选：D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图所示的抛物线是把y=-x2经过平移而得到的．这时抛物线过原点O和x轴正向上一点A，顶点为P，∠OPA=90°；
    ①求抛物线的顶点P的坐标及解析表达式；
    ②求如图所示的抛物线对应的二次函数在-
    1
    2
    ≤x≤
    1
    2
    时的最大值和最小值．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

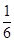    今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定：公共租赁住房和廉租住房并轨运行（以下简称并轨房），计划10年内解决低收入人群住房问题．已知第x年（x为正整数）投入使用的并轨房面积为y百万平方米，且y与x的函数关系式为y=－x+5．由于物价上涨等因素的影响，每年单位面积租金也随之上调．假设每年的并轨房全部出租完，预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表：
    时间x（单位：年，x为正整数）
    		1
    		2
    		3
    		4
    		5
    		…
    单位面积租金z（单位：元/平方米）
    		50
    		52
    		54
    		56
    		58
    		 
     
    （1）求出z与x的函数关系式；
    （2）设第x年政府投入使用的并轨房收取的租金为W百万元，请问政府在第几年投入使用的并轨房收取的租金最多，最多为多少百万元？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    二次函数y=2（x+2）2-3的二次项系数是______，一次项系数是______，常数项是______．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    y=（m2-2m-3）x2+（m-1）x+m2是关于x的二次函数，则m满足的条件是什么？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    二次函数y=ax2+bx+c图象上部分点的坐标满足下表：
    x…-3-2-101…
    y…-3-2-3-6-11…
    则该函数图象的顶点坐标为（　　）
    A．（-3，-3）B．（-2，-2）C．（-1，-3）D．（0，-6）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    下列各式：①y=x+2；②y=2x2；③y=
    2
    x
    ；④y=
    1
    x2
    ；⑤y=(x-1)(x+2)；⑥y=2(x-1)2+2；⑦y    =（2x+1）（x-2）-2x2；其中y是x的二次函数的有______（只填序号）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在直角坐标系中画出函数y=x2-4x-5的图象并回答问题：
    （1）令y=0，可得抛物线与x轴的交点坐标为______
    （2）令x=0，可得抛物线与y轴的交点坐标为______
    （3）把函数y=x2-4x-5配方得y=______可知抛物线开口______，对称轴为______，顶点坐标为
    （4）观察图象，当x______时y随x的增大而______，
    当x______时y随x的增大而______，
    当x=______时，函数有最______值y=______
    （5）观察图象，当y＞0时，x取值范围是______
    （6）观察图象，不等式x2-4x-5＜0的解集是______．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知二次函数y=（x-2a）2+（a-1）（a为常数），当a取不同的值时，其图象构成一个“抛物线系”．如图分别是当a=-1，a=0，a=1，a=2时二次函数的图象．它们的顶点在一条直线上，这条直线的解析式是y=______．

    查看答案和解析>>

    同步练习册答案