
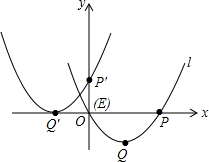
 如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )| A. | (-1,$\frac{1}{2}$) | B. | (0,0) | C. | (-$\frac{1}{2}$,1) | D. | (-$\frac{1}{2}$,0) |
分析 根据图示知,该抛物线经过原点,则易求得该抛物线的解析式,根据该抛物线的解析式和图形可以求得平移规律:该抛物线向上平移了$\frac{1}{2}$个单位、向左平移了1个单位,不难求得点E的对应点了.
解答  解:∵抛物线y=ax2-2x+a2-4经过原点,
解:∵抛物线y=ax2-2x+a2-4经过原点,
∴0=a2-4,
解得 a=±2,
∵抛物线的开口方向向上,
∴a>0,
则a=2.
∴该抛物线的解析式为:y=2x2-2x+22-4=2x(x-1),或y=2(x-$\frac{1}{2}$)2-$\frac{1}{2}$.
∴该抛物线与x轴的交点坐标是O(0,0)、P(1,0),顶点坐标($\frac{1}{2}$,-$\frac{1}{2}$)
依题意得 该抛物线向上平移了$\frac{1}{2}$个单位、向左平移了1个单位,
∴抛物线l与x轴的交点E(0,0)的对应点的坐标为(-1,$\frac{1}{2}$)
故选:A.
点评 本题考查了二次函数图象与几何变换.解题时,利用已知条件得到抛物线的平移规律是解题的难点.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{3}{15}$ | D. | $\frac{5}{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
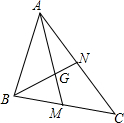 如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).
如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
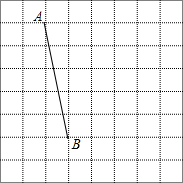 如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.
如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
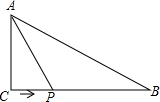 如图,在Rt△ABC中,已知∠C=90°,边AC=4cm,BC=5cm,点P为CB边上一点,当动点P沿CB从点C向点B运动时,△APC的面积发生了变化.
如图,在Rt△ABC中,已知∠C=90°,边AC=4cm,BC=5cm,点P为CB边上一点,当动点P沿CB从点C向点B运动时,△APC的面积发生了变化.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com