
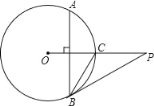
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
【答案】(1)4;(2)详见解析
【解析】
(1)首先连接OB,由弦AB⊥OC,劣弧AB的度数为120°,易证得△OBC是等边三角形,则可求得BC的长;
(2)由OC=CP=4,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP =30°,则可证得OB⊥BP,继而证得PB是⊙O的切线.
(1)连接OB,
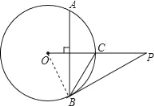
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=4;
(2)证明:∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
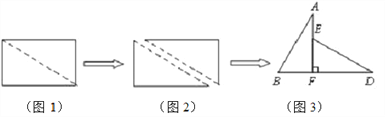
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
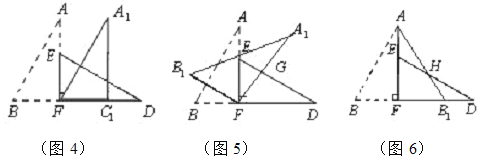
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与x轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程
与x轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程![]() 无实数根;③
无实数根;③![]() ≥0.其中,正确结论的个数为( )
≥0.其中,正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
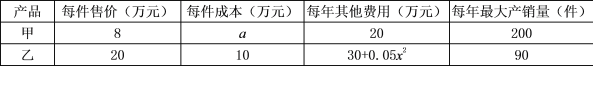
其中a为常数,且5≤a≤7.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与x的函数关系式;(注:年利润=总售价﹣总成本﹣每年其他费用)
与x的函数关系式;(注:年利润=总售价﹣总成本﹣每年其他费用)
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
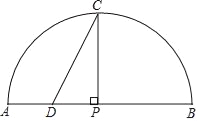
【题目】24如图,P是弧AB所对弦AB上一动点,过点P作PC⊥AB交弧AB于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)
小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小凡的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 |
| 3.2 | 3.4 | 3.3 | 3 |
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点P、Q分别在直线CB与射线DC上(点P不与点C、点B重合),且保持∠APQ=90°,CQ=1,则线段BP的长为_____.
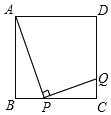
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com