Question

【题目】如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点E，连接OE、AE，过点E作⊙O的切线交边BC于F．

（1）求证：△ODE∽△ECF；

（2）在点O的运动过程中，设DE= ：

①求的最大值，并求此时⊙O的半径长；

②判断△CEF的周长是否为定值，若是，求出△CEF的周长；否则，请说明理由？

Answer 1

【答案】（1）证明见解析；（2）①5；②16.

【解析】试题分析：（1）根据∠OEF=90°得出∠OED+∠CEF=90°，根据∠CEF+∠CFE=90°得出∠OED=∠EFC，最后根据∠D=∠C即可证出△ODE∽△ECF；

（2）①根据△ODE∽△ECF，得出ODCF=DEEC，设DE=x，得出ODCF=-（x-4）2+16，从而求出最大值，设此时半径为r，根据OD2+DE2=OE2，得出（8-r）2+42=r2，解方程即可；

②在Rt△ODE中，根据OD2+DE2=OE2，OA=OE，得出（8-OE）2+x2=OE2，求出OE=4+，OD=4-，根据Rt△DOE∽Rt△CEF，得出，代入得出CF=，EF=，最后根据△CEF的周长=CE+CF+EF代入计算即可得出△CEF的周长=16，是定值．

试题解析：（1）证明：∵EF切⊙O于点M，

∴∠OEF=90°，

∴∠OED+∠CEF=90°，

∵∠C=90°，

∴∠CEF+∠CFE=90°，

∴∠OED=∠EFC，

∵∠D=∠C=90°，

∴△ODE∽△ECF；

（2）解：①由（1）知：△ODE∽△ECF，

∴，

∴ODCF=DEEC，

∵DE=x，

∴EC=8-x，

∴ODCF=x（8-x）=-x2+8x=-（x-4）2+16，

当x=4时，ODCF的值最大，最大值为16，

设此时半径为r，则OA=OE=r，OD=8-r，

在Rt△ODE中，

∵OD2+DE2=OE2，

∴（8-r）2+42=r2，

解得r=5，

即此时半径长为5；

②△CEF的周长为定值，△CEF的周长=16，

在Rt△ODE中，OD2+DE2=OE2，OA=OE，

即：（8-OE）2+x2=OE2，

∴OE=4+，OD=8-OE=4-，

∵Rt△DOE∽Rt△CEF，

即，

∴，

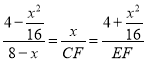解得：CF=，EF=，

∴△CEF的周长=CE+CF+EF=8-x++=16．