
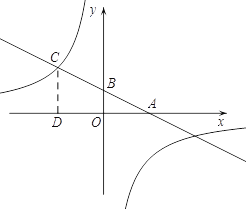
【题目】如图,一次函数的图象与![]() 轴、
轴、![]() 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.

【答案】解:⑴作CD⊥![]() 轴于D,
轴于D,
∴CD∥BO.
∵OA=2OB,
∴OB=2.
∴![]() .
.
∵点B是AC的中点,
∴O是AD的中点.
∴OD=OA=4,CD=2OB=4.
∴点C的坐标为![]() .
.
⑵设反比例函数的解析式为![]() ,
,
∴![]() .
.
∴所求反比例函数的解析式为![]() .
.
设一次函数为![]() ,
,
∵A(4,0),C![]() ,
,
∴![]() 解得:
解得: 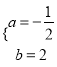 .
.
∴所求一次函数的解析式为![]() .
.
【解析】试题分析:(1)作CD⊥![]() 轴于D,可得CD∥BO.根据点A的坐标为(4,0),OA=2OB,求出B点坐标,根据点B是AC的中点,可知O是AD的中点.即可得到点C的坐标;(2)设反比例函数解析式为
轴于D,可得CD∥BO.根据点A的坐标为(4,0),OA=2OB,求出B点坐标,根据点B是AC的中点,可知O是AD的中点.即可得到点C的坐标;(2)设反比例函数解析式为![]() ,代入C点坐标,解得即可;设一次函数的解析式y=kx+b,将点A、点C的坐标代入,运用待定系数法即可求出一次函数的解析式.
,代入C点坐标,解得即可;设一次函数的解析式y=kx+b,将点A、点C的坐标代入,运用待定系数法即可求出一次函数的解析式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:

(说明:40—55分为不合格,55—70分为合格,70—85分为良好,85—100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
(2)请根据频数分布表,画出相应的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30。 , 求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )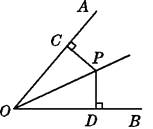
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(多选)下列说法错误的是(__________)
A. 了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查
B. 为了了解全班学生的体温情况,采用全面调查的方式
C. 两直线平行,内错角互补是必然条件
D. 可能性是1%的事件在一次试验中一定不会发生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①不相交的两条直线平行;②一个角的补角一定大于这个角;③从直线外一点作这条直线的垂线段叫做点到这条直线的距离;④同旁内角相等,两直线平行.其中错误的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如图统计图,请根据提供的信息回答问题:

(1)本次调查中,样本容量是 ;
(2)扇形统计图中“基本了解”部分所对应的扇形圆心角是 ;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率的估计值为 ;
(3)请补全频数分布直方图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com