
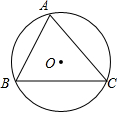
 如图,半径为$\sqrt{2}$的⊙O内接△ABC,∠B=60°,∠C=45°
如图,半径为$\sqrt{2}$的⊙O内接△ABC,∠B=60°,∠C=45°分析 (1)如图1中,连接OA、OB、OC,作OH⊥AC于H,AM⊥BC于M.首先求出AB、AC,再求出AM、BC即可解决问题;
(2)如图2中,延长BE交AC于K,连接BD,EF.只要证明EF是△BCK的中位线即可解决问题;
解答 解:(1)如图1中,连接OA、OB、OC,作OH⊥AC于H,AM⊥BC于M.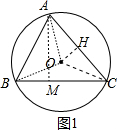
∵∠AOB=2∠ACB=90°,
∴AB=$\sqrt{2}$OA=2,
∵∠AOC=2∠ABC=120°,OA=OC,OH⊥AC,
∴∠AOH=60°,AH=HC=$\frac{\sqrt{6}}{2}$,
∴AC=$\sqrt{6}$,
在Rt△ACM中,AM=CM=$\sqrt{3}$,
在Rt△ABM中,BM=$\frac{1}{2}$AB=1,
∴BCBM+CM=1+$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$•BC•AM=$\frac{1}{2}$•(1+$\sqrt{3}$)•$\sqrt{3}$=$\frac{\sqrt{3}}{2}$+$\frac{3}{2}$.
(2)如图2中,延长BE交AC于K,连接BD,EF.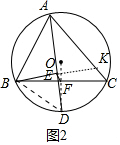
∵D是$\widehat{BC}$的中点,过点D作DF⊥BC于点F,
∴O、F、D共线,BF=FC,
∵∠BED=∠BFD=90°,'
∴B、E、F、F四点共圆,
∴∠EFB=∠BDE=∠ACB=45°,
∴EF∥AC,∵BF=FC,
∴BE=EK,
∴EF=$\frac{1}{2}$CK,
∵∠BAE=∠KAE,∠AEB=∠AEK=90°,
∴∠ABK=∠AKB,
∴AK=AB=2,
∴KC=AC-AK=$\sqrt{6}$-2,
∴EF=$\frac{\sqrt{6}-2}{2}$.
点评 本题考查三角形的外心与外接圆、圆周角定理、解直角三角形、四点共圆、三角形我中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
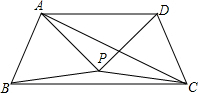 如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).
如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
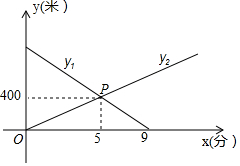 甲从A地出发匀速走向B地,同时乙从B地出发按同一路线匀速走向A地,如图所示,y1、y2分别表示甲、乙离B地的距离(米)与行走时间x(分)之间的关系.
甲从A地出发匀速走向B地,同时乙从B地出发按同一路线匀速走向A地,如图所示,y1、y2分别表示甲、乙离B地的距离(米)与行走时间x(分)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com