
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的是
BF;④AE=BG.其中正确的是

A. ①② B. ①③ C. ①②③ D. ①②③④
【答案】C
【解析】
根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=![]() AC,又因为BF=AC所以CE=
AC,又因为BF=AC所以CE=![]() AC=
AC=![]() BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.故①正确;
在Rt△DFB和Rt△DAC中,
∵∠DBF=90°∠BFD,∠DCA=90°∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
又∵∠BDF=∠CDA=90°,BD=CD,
∴△DFB≌△DAC.
∴BF=AC;DF=AD.
∵CD=CF+DF,
∴AD+CF=BD;故②正确;
在Rt△BEA和Rt△BEC中.
∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵BE=BE,∠BEA=∠BEC=90°,
∴Rt△BEA≌Rt△BEC.
∴CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
∴CE=![]() AC=
AC=![]() BF;故③正确;
BF;故③正确;
连接CG.

∵△BCD是等腰直角三角形,
∴BD=CD.
又DH⊥BC,
∴DH垂直平分BC.∴BG=CG.
在Rt△CEG中,
∵CG是斜边,CE是直角边,
∴CE<CG.
∵CE=AE,
∴AE<BG.故④错误.
故选C.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),则点B′的横坐标是( )
A.6
B.-6
C.3
D.-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD相交于点O , M、N分别是边AB、AD的中点,连接OM、ON、MN , 则下列叙述正确的是( ) 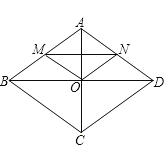
A.△AOM和△AON都是等边三角形
B.四边形MBON和四边形MODN都是菱形
C.四边形AMON和四边形ABCD都是位似图形
D.四边形MBCO和四边形NDCO都是等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC , 支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( ) (栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 . 车辆尺寸:长×宽×高)
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC , AD平分∠BAC , DE∥AC交AB于E , 则S△EBD:S△ABC=( ) 
A.1:2
B.1:4
C.1:3
D.2:3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com