
【题目】P是四边形ABCD内一点,PA=PB=PC=PD,又AB=CD,试确定四边形ABCD的形状,并加以证明.
【答案】解:如图:四边形ABCD是等腰梯形或矩形.
证明如下:
∵PA=PB=PC=PD,AB=CD,
∴△PAB≌△PDC,
∠PAB=∠PBA=∠PCD=∠PDC.
又∵∠PDA=∠PAD,
∴∠BAD=∠CDA.
同理∠ABC=∠DCB.
于是∠BAD+∠ABC= ![]() ×360°=180°,
×360°=180°,
∴AD∥BC.
故当∠ABC≠90°时,四边形ABCD是等腰梯形;
当∠ABC=90°时,四边形ABCD是矩形.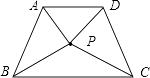
【解析】先证△PAB≌△PDC,再证AD∥BC,然后分情况讨论∠ABC取值可得答案.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形,以及对矩形的判定方法的理解,了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


科目:初中数学 来源: 题型:
【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)若∠B=20°,∠C=80°,求∠EAC和∠EAD的大小.
(2)若∠C>∠B,由(1)的计算结果,你能发现∠EAD与∠C﹣∠B的数量关系吗?写出这个关系式,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+1)x+m2﹣4=0有两个不相等的实数根 (Ⅰ)求实数m的取值范围;
(Ⅱ)若两个实数根的平方和等于15,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的是
BF;④AE=BG.其中正确的是

A. ①② B. ①③ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M , BC边交x轴于点N(如图).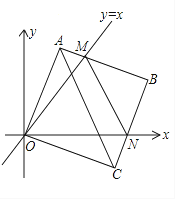
(1)求边OA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p , 在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com