
【题目】在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M , BC边交x轴于点N(如图).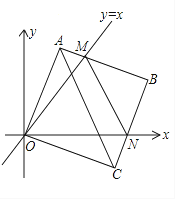
(1)求边OA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p , 在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.
【答案】
(1)
解:∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,
∴OA旋转了45°.
∴OA在旋转过程中所扫过的面积为 ![]()
(2)
解:∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.
∴∠BMN=∠BNM.∴BM=BN.
又∵BA=BC,∴AM=CN.
又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.
∴∠AOM=∠CON= ![]() (∠AOC-∠MON)=
(∠AOC-∠MON)= ![]() (90°-45°)=22.5°.
(90°-45°)=22.5°.
∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°-22.5°=22.5°.
(3)
解:在旋转正方形OABC的过程中,p值无变化.
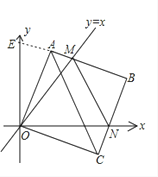
证明:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.
∴△OAE≌△OCN.
∴OE=ON,AE=CN.
又∵∠MOE=∠MON=45°,OM=OM,
∴△OME≌△OMN.∴MN=ME=AM+AE.
∴MN=AM+CN,
∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.
∴在旋转正方形OABC的过程中,p值无变化.
【解析】(1)根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积;(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.


科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1 , 并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2 , 并直接写出C2点的坐标;
(3)作出△ABC关于原点O成中心对称的△A3B3C3 , 并直接写出B3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD相交于点O , M、N分别是边AB、AD的中点,连接OM、ON、MN , 则下列叙述正确的是( ) 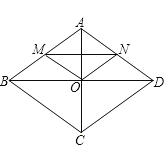
A.△AOM和△AON都是等边三角形
B.四边形MBON和四边形MODN都是菱形
C.四边形AMON和四边形ABCD都是位似图形
D.四边形MBCO和四边形NDCO都是等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏同学想测量一棵大树的高度 . 她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m , 测得仰角为60°,已知小敏同学身高(AB)为1.6m , 则这棵树的高度为( )(结果精确到0.1m , ![]() ≈1.73) .
≈1.73) . 
A.3.5m
B.3.6m
C.4.3m
D.5.1m
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com