
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

【答案】①②④
【解析】
易证△ABD≌△EBC,可得∠BCE=∠BDA,AD=EC可得①②正确,再根据角平分线的性质可求得∠DAE=∠DCE,即AD=AE=EC,根据AD=AE=EC可求得④正确
解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,
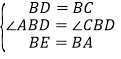 ,
,
∴△ABD≌△EBC(SAS),
∴①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,
∴②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
∵BD为△ABC的角平分线,EF⊥AB,而EC不垂直与BC,
∴EF≠EC,
∴③错误;
④过E作EG⊥BC于G点,
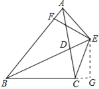
∵E是BD上的点,∴EF=EG,
在Rt△BEG和Rt△BEF中,
![]() ,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
![]() ,
,
∴Rt△CEG≌Rt△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF,
∴④正确.
故答案为:①②④.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M , BC边交x轴于点N(如图).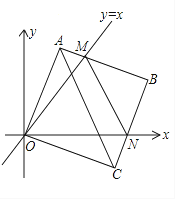
(1)求边OA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p , 在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)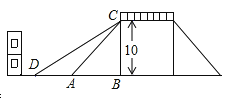
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC , ∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,若BC=7,MN=3,则EF为( ) 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请回答下列问题:
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC , E、F分别是AB , CD的中点,求证:EF= ![]() (AD+BC)
(AD+BC)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H. 
(1)求证:CF=CH;
(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com