
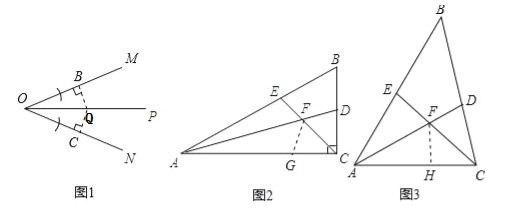
����Ŀ����ͼ1��OP����MON��ƽ���ߣ��������ø�ͼ�λ�һ����OP����ֱ��Ϊ�Գ����ȫ�������Σ��������ӵ�ȫ��������ע��ͼ�ϣ�
����ο������ȫ�������εķ���������������⣺
��1����ͼ2������ABC�У���ACB��ֱ�ǣ���B=60�㣬AD��CE�ֱ�����BAC����BCA��ƽ���ߣ�AD��CE�ཻ�ڵ�F������EFA�Ķ�����
��2���ڣ�1���������£����ж�FE��FD֮���������ϵ����˵�����ɣ�
��3����ͼ3������ABC�У������ACB����ֱ�ǣ����� 1 ���е������������䣬�����ڣ�2�������ý����Ƿ���Ȼ����������������֤����������������˵�����ɣ�

���𰸡���1��60����2��FE=FD��3��FE=FD��Ȼ����
��������
��OM��ON�Ϸֱ��ȡOB��OC��ʹOB=OC���ֱ����B��C��OM��ON�Ĵ��ߣ������߽��ڵ�Q������OQ�����OBQ�ա�OCQ����1����֪��A CB=90�㣬��B=60�������������ε��ڽǺͶ����������BAC=30�㣮����AD��CE�ֱ�����BAC����BCA��ƽ���ߣ����ݽ�ƽ���ߵĶ��������DAC=15�㣬��ECA=45�㣮������������ǵ����ʼ��������EFA=60�㣻��2��FE=FD����AC�Ͻ�ȡAG=AE��֤����EAF�ա�GAF�� ����ȫ�������ε����ʿɵ�FE=FG����EFA=��GFA=60�㣮��֤����DFC=��GFC������ASA�ж���FDC�ա�FGC���ɴ˿ɵ�FD=FG���Ӷ�֤�� FE=FD����3����2���еĽ���FE=FD��Ȼ������֤����ȣ�2���ķ������.
��ͼ��ʾ����OBQ�ա�OCQ��
��1����ͼ2���ߡ�ACB=90�㣬��B=60�㣮
���BAC=30�㣮
��AD��CE�ֱ�����BAC����BCA��ƽ���ߣ�
���DAC=![]() ��BAC=15�㣬��ECA=
��BAC=15�㣬��ECA=![]() ��ACB=45�㣮
��ACB=45�㣮
���EFA=��DAC+��ECA=15��+45��=60�㣮
��2��FE=FD��
��ͼ2����AC�Ͻ�ȡAG=AE������FG��
��AD����BAC��ƽ���ߣ�
���EAF=��GAF��
����EAF����GAF��
��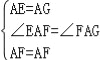
���EAF�ա�GAF��SAS����
��FE=FG����EFA=��GFA=60�㣮
���GFC=180�㩁60�㩁60��=60�㣮
���ߡ�DFC=��EFA=60�㣬
���DFC=��GFC��
����FDC����FGC��
��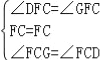
���FDC�ա�FGC��ASA����
��FD=FG��
��FE=FD��
��3����2���еĽ���FE=FD��Ȼ������
ͬ��2���ɵ���EAF�ա�HAF��
��FE=FH����EFA=��HFA��
���ɣ�1��֪��FAC=![]() ��BAC����FCA=
��BAC����FCA=![]() ��ACB��
��ACB��
���FAC+��FCA=![]() ����BAC+��ACB��=
����BAC+��ACB��=![]() =60�㣮
=60�㣮
���AFC=180�㩁����FAC+��FCA��=120�㣮
���EFA=��HFA=180�㩁120��=60�㣮
ͬ��2���ɵ���FDC�ա�FHC��
��FD=FH��
��FE=FD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У�ֱ��AB����CD�ཻ�ڵ�P����CAB=40�㣬��APD=65�㣮 
��1�����B�Ĵ�С��
��2����֪Բ��0��BD�ľ���Ϊ3����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڳ�����ABCD�У�AB=4��AD=6���ӳ�BC����E��ʹCE=2������DE������P�ӵ�B��������ÿ��2����λ���ٶ���BC��CD��DA���յ�A�˶������P���˶�ʱ��Ϊt�룬��t��ֵΪ_____��ʱ����ABP����DCEȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪P(3��3)����B��A�ֱ���x���������y���������ϣ���APB��90������OA��OB��________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����y=mx+m��y=��mx2+2x+2��m�dz�������m��0����ͼ������ǣ� ��
A.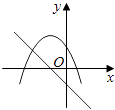
B.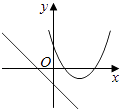
C.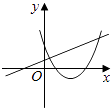
D.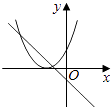
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����2m+1��x+m2��4=0����������ȵ�ʵ���� ������ʵ��m��ȡֵ��Χ��
����������ʵ������ƽ���͵���15����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=30�㣬��ֱ�Ƕ���AΪԲ�ģ�AB��Ϊ�뾶������BC�ڵ�D����D��DE��AC�ڵ�E����DE=a�����ABC���ܳ��ú�a�Ĵ���ʽ��ʾΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��߳�Ϊ2��������OABC��������A��C�ֱ���y�ᡢx����������ϣ���O��ԭ�㣮�ֽ�������OABC��O��˳ʱ����ת����A���һ������ֱ��y=x��ʱֹͣ��ת����ת�����У�AB�߽�ֱ��y=x�ڵ�M �� BC�߽�x���ڵ�N����ͼ����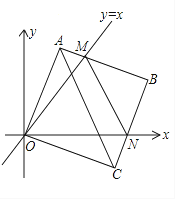
��1�����OA����ת��������ɨ���������
��2����ת�����У���MN��ACƽ��ʱ����������OABC��ת�Ķ�����
��3�����MBN���ܳ�Ϊp �� ����ת������OABC�Ĺ����У�pֵ�Ƿ��б仯����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������ŵ�ʾ��ͼ�����ŵĸ߶���10�ף�CB��DB �� ����AC����б��Ϊ45�� �� Ϊ�˷��������Ƴ������ţ��������ž��������¶ȣ�ʹ������DC���¶�Ϊi= ![]() ��3 �� �����½�������3�������е�������ԭ�½ǣ�A�㴦��10�Ľ������Ƿ���Ҫ��������ο����ݣ�
��3 �� �����½�������3�������е�������ԭ�½ǣ�A�㴦��10�Ľ������Ƿ���Ҫ��������ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��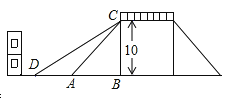
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com