
 已知抛物线 y=x2-2x-3
已知抛物线 y=x2-2x-3分析 (1)把解析式化为顶点式,则可求得其顶点坐标及其对称轴,令y=0可求得x,则可求得与x轴的交点坐标,令x=0可求得与y轴的交点坐标;
(2)利用(1)中确定的几个关键点可作出函数图象;
(3)结合图象可求得答案.
解答 解:
(1)∵y=x2-2x-3=(x-1)2-4,
∴抛物线顶点坐标为(1,-4),对称轴为x=1,
令y=0可得x2-2x-3=0,解得x=3或-1,
∴抛物线与x轴的交点坐标为(3,0)和(-1,0),
令x=0可得y=-3,
∴抛物线与y轴的交点坐标为(0,-3),
故答案为:(1,-4);(3,0);(-1,0);(0,-3);x=1;
(2)利用(1)所求的四个点,结合对称轴画出其图象,如图,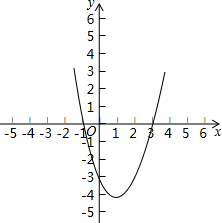
(3)由图象可知当x<1时,y随x的增大而减小.
点评 本题主要考查二次函数的图象和性质,化一般式为顶点式是解题的关键,注意数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,BD=CD.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,BD=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
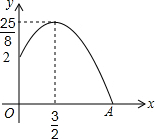 某公园有一喷水池,已知喷水管高2m,喷水最高高度为$\frac{25}{8}$m,此时喷水的水平距离为$\frac{3}{2}$m,求圆形水池的半径.
某公园有一喷水池,已知喷水管高2m,喷水最高高度为$\frac{25}{8}$m,此时喷水的水平距离为$\frac{3}{2}$m,求圆形水池的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形DEFG的边DE与等腰直角三角形ABC的斜边AB均在直线l上,点B与点D重合,DE=4,AB=2.若正方形DEFG保持不动,△ABC沿直线l向右以每秒1个单位的速度匀速滑动,试写出从△ABC开始滑动到与正方形DEFG完全脱离开的两图形重叠部分的面积S与滑动时间t的函数表达式.
如图,已知正方形DEFG的边DE与等腰直角三角形ABC的斜边AB均在直线l上,点B与点D重合,DE=4,AB=2.若正方形DEFG保持不动,△ABC沿直线l向右以每秒1个单位的速度匀速滑动,试写出从△ABC开始滑动到与正方形DEFG完全脱离开的两图形重叠部分的面积S与滑动时间t的函数表达式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com