
【题目】(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN2,ND2,DH2之间的数量关系,并说明理由.
(3)在图①中,若EG=4,GF=6,求正方形ABCD的边长.

【答案】(1) 45°.(2) MN2=ND2+DH2.理由见解析;(3)12.
【解析】
试题分析:(1)先根据AG⊥EF得出△ABE和△AGE是直角三角形,再根据HL定理得出△ABE≌△AGE,故可得出∠BAE=∠GAE,同理可得出∠GAF=∠DAF,由此可得出结论;
(2)由旋转的性质得出∠BAM=∠DAH,再根据SAS定理得出△AMN≌△AHN,故可得出MN=HN.再由∠BAD=90°,AB=AD可知∠ABD=∠ADB=45°,根据勾股定理即可得出结论;
(3)设正方形ABCD的边长为x,则CE=x-4,CF=x-6,再根据勾股定理即可得出x的值.
试题解析:(1)在正方形ABCD中,∠B=∠D=90°,
∵AG⊥EF,
∴△ABE和△AGE是直角三角形.
在Rt△ABE和Rt△AGE中,
![]() ,
,
∴△ABE≌△AGE(HL),
∴∠BAE=∠GAE.
同理,∠GAF=∠DAF.
∴∠EAF=∠EAG+∠FAG=![]() ∠BAD=45°.
∠BAD=45°.
(2)MN2=ND2+DH2.
由旋转可知:∠BAM=∠DAH,
∵∠BAM+∠DAN=45°,
∴∠HAN=∠DAH+∠DAN=45°.
∴∠HAN=∠MAN.
在△AMN与△AHN中,
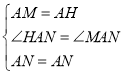 ,
,
∴△AMN≌△AHN(SAS),
∴MN=HN.
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°.
∴∠HDN=∠HDA+∠ADB=90°.
∴NH2=ND2+DH2.
∴MN2=ND2+DH2.
(3)由(1)知,BE=EG=4,DF=FG=6.
设正方形ABCD的边长为x,则CE=x-4,CF=x-6.
∵CE2+CF2=EF2,
∴(x-4)2+(x-6)2=102.
解这个方程,得x1=12,x2=-2(不合题意,舍去).
∴正方形ABCD的边长为12.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】给出4个命题:①三边对应成比例的两个三角形相似;②两边对应成比例且一个角对应相等的两个三角形相似;③一个锐角对应相等的两个直角三角形相似;④一个角相等的两个等腰三角形相似,其中正确的命题是( )
A. ①③ B. ①④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在第四象限,距离x轴4个单位长度,距离y轴2个单位长度,则点P的坐标是( )
A. (4,-2) B. (2,-4) C. (-4,2) D. (-2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2-8x+15=0,左边化成含有x的完全平方形式,其中正确的是( ).
A. x2-8x+(-4)2=31 B. x2-8x+(-4)2=1 C. x2+8x+42=1 D. x2-4x+4=-11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com