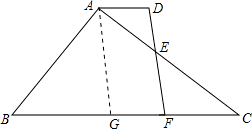
解:(1)△ABC∽△FEC∽△DEA.(1分)
证明如下:∵AD∥BC,
∴∠DAE=∠C,(1分)
又∵∠FEC=∠DEA=∠B,
∴△ABC∽△FEC∽△DEA;(1分)
(2)过点A作AG∥DF,AG与BC相交于点G,
∴∠GAC=∠DEA.(1分)
∵∠DEA=∠B,
∴∠GAC=∠B,
∴△GAC∽△ABC,(1分)
∴AG:AB=AC:BC,
∴AG:8=12:16,
∴AG=6.(1分)
∵AD∥BC,AG∥DF,
∴四边形AGFD是平行四边形,
∴DF=AG=6;(1分)
(3)∵DE=x,
∴EF=6-x,
由△ABC∽△FEC,CF:EF=AC:AB,
CF:(6-x)=12:8,(1分)
CF=
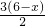
,BF=BC-CF=16-
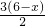
,(1分)
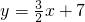
(0<x<6).(1分)
分析:(1)根据相似三角形的判定定理:两角对应相等,两三角形相似,可知图中的相似三角形有:△ABC∽△FEC∽△DEA;
(2)作辅助线AG(过点A作AG∥DF,AG与BC相交于点G)构建平行四边形ADFG,由平行四边形的对边相等求得DF=AG=6;
(3)根据相似三角形△ABC∽△FEC的对应边成比例知CF:EF=AC:AB,而BF=BC-CF,所以据此可以列出关于y与x之间的函数解析式,由DE的取值范围来确定该函数的定义域.
点评:本题考查了相似三角形的判定与性质.解答此题时,通过构建与已知和所求的条件相关的三角形,然后证明其相似来得出线段间的比例关系.

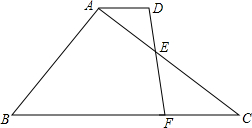 ∠B,DE的延长线交BC边于F.
∠B,DE的延长线交BC边于F. 解:(1)△ABC∽△FEC∽△DEA.(1分)
解:(1)△ABC∽△FEC∽△DEA.(1分)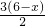 ,BF=BC-CF=16-
,BF=BC-CF=16-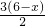 ,(1分)
,(1分)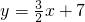 (0<x<6).(1分)
(0<x<6).(1分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为