
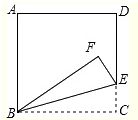
 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°. 分析 根据翻折的性质可得∠BEF=∠BEC,∠EBF=∠EBC,然后求出∠BEC,再根据直角三角形两锐角互余求出∠EBC,然后根据∠ABF=90°-∠EBF-∠EBC代入数据进行计算即可得解.
解答  解:补全正方形如图,
解:补全正方形如图,
由翻折的性质得,∠BEF=∠BEC,∠EBF=∠EBC,
∵∠DEF=30°,
∴∠BEC=$\frac{1}{2}$(180°-∠DEF)=$\frac{1}{2}$(180°-40°)=70°,
∴∠EBC=90°-∠BEC=90°-70°=20°,
∴∠ABF=90°-∠EBF-∠EBC
=90°-20°-20°
=50°.
故答案为:50°.
点评 本题考查了翻折变换的性质,正方形的性质,熟记翻折变换前后的图形能够重合是解题的关键,难点在于作辅助线补全正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 7 | C. | 8或1 | D. | 7或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 类比思想 | B. | 转化思想 | C. | 方程思想 | D. | 函数思想 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读与计算:请阅读以下材料,并完成相应的任务.
阅读与计算:请阅读以下材料,并完成相应的任务.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=$\frac{4}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=2x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
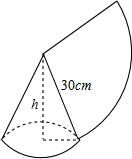 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com