
 �Ķ�����㣺���Ķ����²��ϣ��������Ӧ������
�Ķ�����㣺���Ķ����²��ϣ��������Ӧ���������� ��1����a��b��c�ij��������S2���ٿ������㼴�ɵý⣻
��2����a��b��c�ij��������S2���ٿ������㼴�ɵý⣮
��� �⣺��1��p=$\frac{a+b+c}{2}$=$\frac{5+6+7}{2}$=9��
S=$\sqrt{p��p-a����p-b����p-c��}$
=$\sqrt{9����9-5������9-6������9-7��}$
=6$\sqrt{6}$��
�����������������6$\sqrt{6}$��
��2��S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-��\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}��^{2}]}$
=$\sqrt{\frac{1}{4}[{��\sqrt{5}��}^{2}{����\sqrt{6}��}^{2}-��\frac{��{\sqrt{5}��}^{2}+��\sqrt{6}��^{2}-��{\sqrt{7}��}^{2}}{2}��^{2}]}$
=$\sqrt{\frac{1}{4}[5��6-��\frac{5+6-7}{2}��^{2}]}$
=$\sqrt{\frac{1}{4}��30-4��}$
=$\frac{\sqrt{26}}{2}$��
���������������$\frac{\sqrt{26}}{2}$��
�ʴ�Ϊ��6$\sqrt{6}$��
���� ���⿼���˶��θ�ʽ��Ӧ�ã��ѵ����ڶԸ���������������ƽ�����Ķ�����㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�ľ���ֵ��-1 | B�� | 1�ĵ�����-1 | C�� | 1���෴����-1 | D�� | 1��ƽ������-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+x3=x6 | B�� | 2x+3y=5xy | C�� | ��x3��2=x6 | D�� | x6��x3=x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
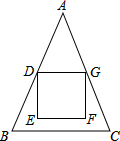 ��ͼ��С����һ���߳�Ϊ10��������DEFG��ֽ���ڡ�ABCֽƬ�ϣ�����AB=AC=26��BC=20�������εĶ���D��G�ֱ��ڱ�AB��AC�ϣ���AD=AG����E��F�ڡ�ABC�ڲ������E��BC�ľ���Ϊ��������
��ͼ��С����һ���߳�Ϊ10��������DEFG��ֽ���ڡ�ABCֽƬ�ϣ�����AB=AC=26��BC=20�������εĶ���D��G�ֱ��ڱ�AB��AC�ϣ���AD=AG����E��F�ڡ�ABC�ڲ������E��BC�ľ���Ϊ��������| A�� | 1 | B�� | 2 | C�� | $\sqrt{21}$ | D�� | $\sqrt{29}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
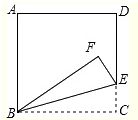 ��ͼ����������ֽƬABCD��BE���ۣ�ʹ��C���ڵ�F��������DEF=40�㣬���ABF�Ķ���Ϊ50�㣮
��ͼ����������ֽƬABCD��BE���ۣ�ʹ��C���ڵ�F��������DEF=40�㣬���ABF�Ķ���Ϊ50�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢۢ� | B�� | �٢ۢ� | C�� | �٢� | D�� | �٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
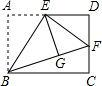 ��ͼ������ABCD�У�E��AD���е㣬����ABE��ֱ��BE�۵���õ���GBE���ӳ�BG��CD�ڵ�F����AB=6��BC=4$\sqrt{6}$����FD�ij�Ϊ4��
��ͼ������ABCD�У�E��AD���е㣬����ABE��ֱ��BE�۵���õ���GBE���ӳ�BG��CD�ڵ�F����AB=6��BC=4$\sqrt{6}$����FD�ij�Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������1.8 | B�� | ������3 | C�� | ��λ����3 | D�� | ƽ������3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com