
 已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.分析 (1)作DF⊥OB于点F,在直角△ODF中利用三角函数求得DF和OF的长,则D的坐标即可求得,然后根据CD∥OB,则C的坐标即可求得;
(2)B关于OC的对称点是D,则DE的长就是PE+PB的最小值,作DH⊥y轴于点H,首先在直角△OGH中利用勾股定理求得DH和OH的长,然后在直角△HED中利用勾股定理求解.
解答 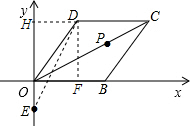 解:(1)作DF⊥OB于点F.
解:(1)作DF⊥OB于点F.
∵B的坐标是(2,0),
∴OB=2,
∴菱形OBCD中,OD=OB=CD=2,
在直角△ODF中,DF=OD•sin∠DOB=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,OF=OD•cos∠DOB=2×$\frac{1}{2}$=1,
则D的坐标是(1,$\sqrt{3}$).
则C的坐标是(3,$\sqrt{3}$).
故答案是:(1,$\sqrt{3}$),(3,$\sqrt{3}$);
(2)作DH⊥x轴于点H,连接DE.
在直角△OGH中,∠HOG=90°-∠DOB=90°-60°=30°.
GH=OD•sin∠HOG=2×$\frac{1}{2}$=1,OH=OG•cos∠HOG=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
则HE=2$\sqrt{3}$.
在直角△HEG中,DE=$\sqrt{H{G}^{2}+H{E}^{2}}$=$\sqrt{{1}^{2}+(2\sqrt{3})^{2}}$=$\sqrt{13}$.
即PE+PB的最小值是$\sqrt{13}$.
点评 本题考查了菱形的性质以及路径最短问题,根据菱形的对称性确定PE+PB最小的条件是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 21 | B. | $\frac{1}{21}$ | C. | 7 | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)先化简,再求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$,其中x=2016.
(1)先化简,再求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$,其中x=2016.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com