已知四边形ABCD的面积为32,AB、CD、AC的长都是整数,且它们的和为16.
(1)这样的四边形有几个?
(2)求这样的四边形边长的平方和的最小值.
分析:(1)根据题意画出图形,再根据S四边形ABCD=S△ABC+S△ADC,列出关于a、b、l的不等式,
求出当四边形ABCD面积最大时未知数的值即可;
(2)根据四边形面积最大时△ABC及△ACD均为直角三角形,利用勾股定理即可求出四边形边长的平方和的最小值.
解答: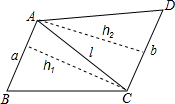
解:(1)如图,记AB=a,CD=b,AC=l,并设△ABC的边BA上的高为h
1,△ADC的边DC上的高为h
2,
则S
四边形ABCD=S
△ABC+S
△ADC=
(h
1a+h
2b)≤
l(a+b),
当且仅当h
1=h
2=l时等号成立,即在四边形ABCD中,当AC⊥AB,AC⊥CD时,等号成立,
由已知得64≤l(a+b),又∵a+b=16-l,
得64≤l(16-l)=64-(l-8)
2≤64,
于是l=8,a+b=8,且这时AC⊥AB,AC⊥CD,
因此这样的四边形由如下4个:a=1,b=7,l=8;a=2,b=6,l=8;a=3,b=5,l=8;a=b=4,l=8;
(2)由于AB=a,CD=8-a,则BC
2=8
2+a
2,AD
2=8
2+(8-a)
2,
故这样的四边形的边长的平方和为:
2a
2+2(8-a)
2+128=4(a-4)
2+192,
当a=b=4时,平方和最小,且为192.
故答案为:4,192.
点评:本题考查的是等积变换,解答此题的关键是把四边形的面积转化为三角形的面积,再利用三角形的面积及勾股定理求解.

 解:(1)如图,记AB=a,CD=b,AC=l,并设△ABC的边BA上的高为h1,△ADC的边DC上的高为h2,
解:(1)如图,记AB=a,CD=b,AC=l,并设△ABC的边BA上的高为h1,△ADC的边DC上的高为h2,

 阅读快车系列答案
阅读快车系列答案 如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )
如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )