
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
【答案】A
【解析】首先利用勾股定理计算出AC的长,再根据折叠可得△DEC≌△D′EC,设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,再根据勾股定理可得方程22+x2=(4﹣x)2,再解方程即可.
解:∵AB=3,AD=4,
∴DC=3,
∴AC=![]() =5,
=5,
根据折叠可得:△DEC≌△D′EC,
∴D′C=DC=3,DE=D′E,
设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,
在Rt△AED′中:(AD′)2+(ED′)2=AE2,
22+x2=(4﹣x)2,
解得:x=![]() ,
,
故选:A.
“点睛”此题主要考查了图形的翻着变换,以及勾股定理的应用,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:
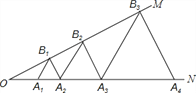
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
(1)点B关于坐标原点O对称的点的坐标为 ( );
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B、B1的一次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
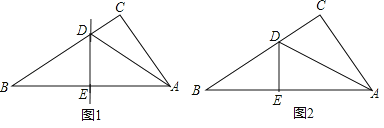
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是 ( )
A. (2a2)3=6a6 B. a3.a2=a5 C. 2a2+4a2=6a4 D. (a+2b)2=a2+4b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知点A (1,2),B (-2, 2), C (-2, -2), D (1 ,-2), 把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→D→C→B→A……的顺序紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是 ( )

A. (1, 2 ) B. ( 0, 2 ) C. (1,1) D. (1 ,-2 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定四边形是平行四边形的是( )
A. 对角线互相平分B. 两组对边分别相等
C. 对角线互相垂直D. 一组对边平行,一组对角相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com