
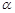 (0°<
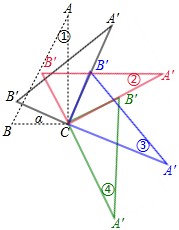
(0°<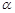 <180°).若△A′B′C中恰有一条边与△ABC中的一条边平行,则旋转角
<180°).若△A′B′C中恰有一条边与△ABC中的一条边平行,则旋转角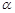 的可能的度数为 .
的可能的度数为 . 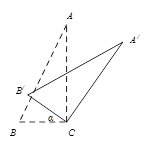


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 ,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n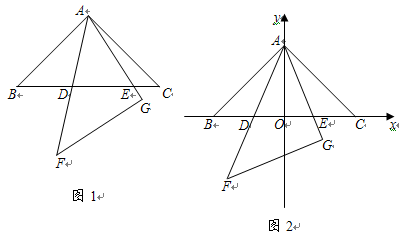
 ;
; 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′,则
,将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′,则 =( )
=( )| A.60° | B.105° | C. 120° | D. 135° |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com