
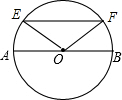
 如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.
如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$和$\sqrt{2}$ | B. | $\sqrt{54}$和$\sqrt{108}$ | C. | $\sqrt{8a}$和$\sqrt{32a}$ | D. | $\sqrt{63}$和$\sqrt{112}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,DF∥AC,DE∥BC,下列各式中正确的有( )
如图,DF∥AC,DE∥BC,下列各式中正确的有( )| A. | (1)(2) | B. | (1)(3) | C. | (1)(2)(3) | D. | (1)(2)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11+[(-13)+7]=17 | B. | (-2.5)+[5+(-2.5)]=5 | C. | [3$\frac{1}{2}$+(-3$\frac{1}{2}$)]+(-2)=-2 | D. | 3.14+[(-4)+3.14]=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两数的差为0,则这两数必相等 | |
| B. | 较大的数减去较小的数,差一定是正数 | |
| C. | 两数之差一定小于被减数 | |
| D. | 减去一个负数,差一定大于被减数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com