
【题目】已知⊙O和⊙O上的一点A(如图).
(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题的作图中,如果点E在![]() 上,求证:DE是⊙O内接正十二边形的边.
上,求证:DE是⊙O内接正十二边形的边.

【答案】(1)作图见解析(2)证明见解析
【解析】试题分析:(1)根据定理将⊙O的圆周角平均分成四等分和六等分,其中四等分的方法是两条直径互相垂直,由垂径定理可知把圆四等分,而六等分分成的正六边形的边长等于半径.
(2)要证DE为⊙O的内接正十二边形的一边,只需证明DE所对圆心角等于30°即可.
试题解析: (1)作法:
①作直径AC,
②作直径BD⊥AC,
③依次连接A,B,C,D四点,
四边形ABCD即为⊙O的内接正方形,
①分别以A,C为圆心,OA的长为半径作弧,交⊙O于E,H,F,G,
②顺次连接A,E,F,C,G,H各点,
六边形AEFCGH为⊙O的内接正六边形.
(2)连接OE,DE,
∵∠AOD=![]() =90°,∠AOE=
=90°,∠AOE=![]() =60°,
=60°,
∴∠DOE=∠AOD-∠AOE=30°,
∴ DE为⊙O的内接正十二边形的一边.


科目:初中数学 来源: 题型:
【题目】如图,∠1=60,∠2=60,∠3=57,则∠4=57,下面是A,B,C,D四个同学的推理过程,你认为推理正确的是( )

A.因为∠1=60=∠2,所以a∥b,所以∠4=∠3=57
B.因为∠4=57=∠3,所以a∥b,故∠1=∠2=60
C.因为∠2=∠5,又∠1=60,∠2=60,故∠1=∠5=60,所以a∥b,所以∠4=∠3=57
D.因为∠1=60,∠2=60,∠3=57,所以∠1=∠3=∠2-∠4=60-57=3,
故∠4=57
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两队进行足球对抗赛,比赛的规则规定每队胜一场得3分,平一场得1分,负一场得0分.两队一共进行10场比赛,甲队未负一场,得分超过22分.甲队至少胜了多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据重庆商报2016年5月23日报道,第十九届中国(重庆)国际投资暨全球采购会(简称渝洽会)集中签约86个项目,投资总额1636亿元人民币,将数1636用科学记数法表示是( )
A.0.1636×104
B.1.636×103
C.16.36×102
D.163.6×10
查看答案和解析>>
科目:初中数学 来源: 题型:
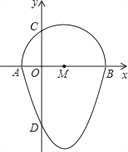
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用计算器求图中∠A的正弦值、余弦值、正切值.
(2)已知sin A=0.328 6,tan B=10.08,利用计算器求锐角A,B.(结果精确到0.01°)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com