
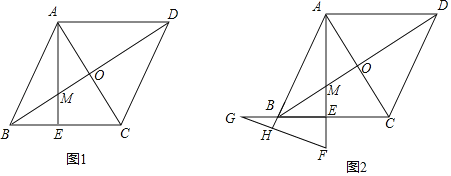
【题目】在平行四边形ABCD中,对角线AC、BD交于点O,若AB=BC,过点A作BC的垂线交BC于点E,交BD于点M,∠ABC>60°.
(1)若ME=3,BE=4,求EC的长度.
(2)如图,延长CE至点G;使得EC=GE;过点G作GF垂直于AB的延长线于点H,交AE的延长线于点F,
求证:AE=GF+EF.
【答案】(1)CE=![]() ;(2)见解析
;(2)见解析
【解析】
(1)由邻边相等的平行四边形得出四边形ABCD是菱形,得出AC⊥BD,∠BOC=90°,OA=OC,OB=OD,证出∠MBE=∠CAE,证得△MBE∽△CAE,得出![]() =
=![]() =
=![]() ,由勾股定理求出MB=
,由勾股定理求出MB=![]() =5,则
=5,则![]() =
=![]() =
=![]() ,设CE=3k,则CA=5k,CO=
,设CE=3k,则CA=5k,CO=![]() AC=
AC=![]() ,CB=CE+EB=3k+4,由sin∠OBC=
,CB=CE+EB=3k+4,由sin∠OBC=![]() =
=![]() ,sin∠MBE=
,sin∠MBE=![]() =
=![]() ,∠MBE=∠OBC,得出
,∠MBE=∠OBC,得出![]() =
=![]() ,求出k=
,求出k=![]() ,即可得出结果;
,即可得出结果;
(2)连接CM,易证M是△ABC的三条高的交点,即CM⊥AB,推出GH∥CM,即GF∥CM,得出∠CME=∠GFE,由AAS证得△CME≌△GFE,得出CM=GF,EM=EF,由垂直平分线的性质得出MC=MA,推出GF=MA,即可得出结论.
(1)解:∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,∠BOC=90°,OA=OC,OB=OD,
∴∠MBE+∠ACE=90°,
∵AE⊥BC,
∴∠AEC=∠BEM=90°,∠CAE+∠ACE=90°,
∴∠MBE=∠CAE,
∴△MBE∽△CAE,
∴![]() =
=![]() =
=![]() ,
,
MB=![]() =
=![]() =5,
=5,
∴![]() =
=![]() =
=![]() ,
,
设CE=3k,则CA=5k,
∴CO=![]() AC=
AC=![]() ,
,
CB=CE+EB=3k+4,
∵sin∠OBC=![]() =
=![]() ,sin∠MBE=
,sin∠MBE=![]() =
=![]() ,∠MBE=∠OBC,
,∠MBE=∠OBC,
∴![]() =
=![]() ,
,
∴k=![]() ,
,
∴CE=3k=![]() ;
;
(2)证明:连接CM,如图2所示:
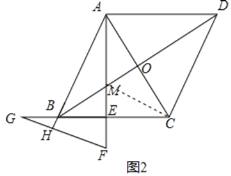
∵AE⊥BC,BO⊥AC,AE与BO交于M,
∴M是△ABC的三条高的交点,即CM⊥AB,
∵GH⊥AB,
∴GH∥CM,即GF∥CM,
∴∠CME=∠GFE,
在△CME和△GFE中,
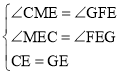 ,
,
∴△CME≌△GFE(AAS),
∴CM=GF,EM=EF,
∵BD⊥AC,OA=OC,
∴MC=MA,
∴GF=MA,
∵AE=AM+ME,
∴AE=GF+EF.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.
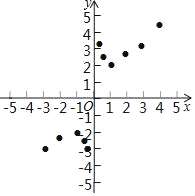
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.
(1)张华用“微信”支付的概率是______.
(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月的第二个周日是母亲节,丁丁精心地设计了一份手工礼物送给妈妈.为了尽快完成手工礼物,丁丁骑自行车到位于家正东方向的商店购买材料.丁丁离家5分钟后自行车出现故障,丁丁立即打电话通知在家看报纸的爸爸带上工具箱来帮忙维修(丁丁打电话和爸爸找工具箱的时间忽略不计),同时丁丁以原来一半的速度推着自行车继续走向商店.爸爸接到电话后,立刻出发追赶丁丁,追上丁丁后,爸爸用2分钟的时间修好了自行车,并立刻以原速到位于家正西方500米的公司上班(爸爸换电话的时间忽略不计),丁丁则以原来的骑车速度到达商店.在整个过程中,丁丁和爸爸保持匀速行驶.如图是丁丁、爸爸的距离y(米)与丁丁的出发时间x(分钟)之间的函数图象,则爸爸到达公司时,丁丁距离商店_____米.
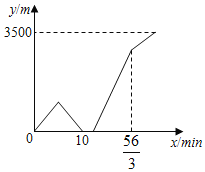
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC.
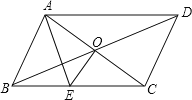
(1)若△ABE的周长为10cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长是8,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是( )
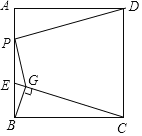
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过点A(4,0)、B(﹣2,0)、C(0,﹣4)
(1)求抛物线的解析式;
(2)在抛物线AC段上是否存在点M,使△ACM的面积为3,求出在此时M的坐标,若不存在,说明理由.
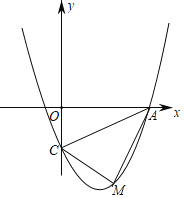
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )

A. 以相同速度行驶相同路程,甲车消耗汽油最多
B. 以10km/h的速度行驶时,消耗1升汽油,甲车最少行驶5千米
C. 以低于80km/h的速度行驶时,行驶相同路程,丙车消耗汽油最少
D. 以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com