
 如图,直线y=x与抛物线y=x2-x-3交于A、B两点,点P是抛物线上的一个动点,过点P作直线PQ⊥x轴,交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随m的增大而减小时m的取值范围是
如图,直线y=x与抛物线y=x2-x-3交于A、B两点,点P是抛物线上的一个动点,过点P作直线PQ⊥x轴,交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随m的增大而减小时m的取值范围是
 <x<3
<x<3 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
 如图,小明把小球竖直向上抛起,当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置,且灯与球心所在直线垂直于地面,这时小球在地面的影子的面积为1.92πm2.已知,灯与地面的距离为2.4m,小球的半径为
如图,小明把小球竖直向上抛起,当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置,且灯与球心所在直线垂直于地面,这时小球在地面的影子的面积为1.92πm2.已知,灯与地面的距离为2.4m,小球的半径为查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:河南省期中题 题型:解答题
 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知m、n是方程![]() 的两个实数根,且m<n,抛物线
的两个实数根,且m<n,抛物线![]() 的图像经过点A(m,0)、B(0,n).
的图像经过点A(m,0)、B(0,n).
 (1)求这个抛物线的解析式;
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的
顶点为D,试求出点C、D的坐标和△BCD的面积;
(注:抛物线![]() 的顶点坐标为
的顶点坐标为
![]()
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛
物线交于H点,若直线BC把△PCH分成面积之比
为2:3的两部分,请求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:解答题
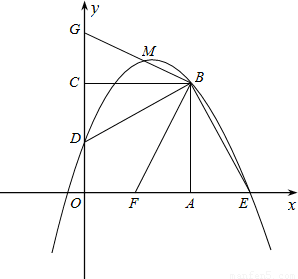
在平面直角坐标xOy中,(如图)正方形OABC的边长为4,边OA在x轴的正半轴上,边OC在y轴的正半轴上,点D是OC的中点,BE⊥DB交x轴于点E.
⑴求经过点D、B、E的抛物线的解析式;
⑵将∠DBE绕点B旋转一定的角度后,边BE交线段OA于点F,边BD交y轴于点G,交⑴中的抛
物线于M(不与点B重合),如果点M的横坐标为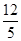 ,那么结论OF=
,那么结论OF=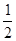 DG能成立吗?请说明理由.
DG能成立吗?请说明理由.
⑶过⑵中的点F的直线交射线CB于点P,交⑴中的抛物线在第一象限的部分于点Q,且使△PFE为等腰三角形,求Q点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com