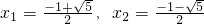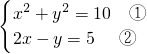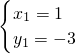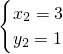解:(1)方程整理为:(x-1)
2=9
x-1=±3
x=1±3
∴x
1=4,x
2=-2;
(2)2x
2-4x-1=0
a=2,b=-4,c=-1,
△=16+8=24
x=

∴

;
(3)方程化为:
(3x+4)(2x-3)=0
3x+4=0或2x-3=0
∴
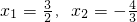
;
(4)x
2-6x=391
x
2-6x+9=400
(x-3)
2=400
x-3=±20
x=3±20
∴x
1=23,x
2=-17;
(5)方程整理为:(x
2+x)
2+2(x
2+x)-3=0
(x
2+x+3)(x
2+x-1)=0
x
2+x+3=0
∵△=1-12<0,∴无解.
x
2+x-1=0
△=1+4=5
x=
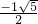
经检验
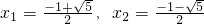
是原方程的根.
∴
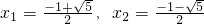
(6)方程组:
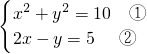
方程②化为:y=2x-5 ③
把③代入①整理得:
x
2-4x+3=0
(x-1)(x-3)=0
∴x
1=1,x
2=3.
把x
1,x
2代入③得:y
1=-3,y
2=1.
∴
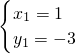
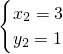
分析:(1)把方程整理后用直接开平方法解方程.(2)用一元二次方程的求根公式求出方程的根.(3)用十字相乘法因式分解求出方程的根.(4)把常数项移到右边,用配方法解方程.(5)把x
2+x看成是一个整体,先用十字相乘法因式分解求出x
2+x的值,然后再解关于x的方程.(6)用代入消元法解方程组.
点评:本题考查的是解方程和方程组,(1)题用直接开平方法解方程.(2)题用一元二次方程的求根公式求出方程的根.(3)题用十字相乘法因式分解求出方程的根.(4)题用配方法求出方程的根.(5)把x
2+x看成是一个整体,用十字相乘法因式分解解关于x
2+x的一元二次方程,然后再解关于x的一元二次方程.(6)题用代入法解方程组.

 ;
; ;
;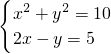 .
.
 ;
;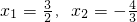 ;
;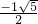
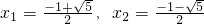 是原方程的根.
是原方程的根.