Question

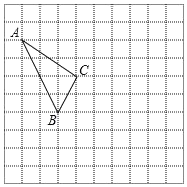
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4，4)，(﹣1，2)．

(1)请在如图所示的网格平面内作出平面直角坐标系；

(2)将△ABC向右平移2个单位长度，然后再向下平移3个单位长度，得到△A′B′C′，画出平移后的△A′B′C′．

(3)求S△A′B′C′的面积．

Answer 1

【答案】(1)见解析；(2)见解析；(3)S△A′B′C′＝4.

【解析】

（1）根据点A、点C的坐标确定出坐标原点，然后建立平面直角坐标系即可；（2）根据网格结构找出平移后的点A′、B′、C′的位置，然后顺次连接即可；（3）根据三角形的面积等于三角形所在的矩形的面积减去四周三个直角三角形的面积，列式计算即可得解.

解：(1)如图，建立平面直角坐标系；

(2)如图，△A′B′C′为所作；

(3)S△A′B′C′＝3×4﹣×2×1﹣×2×3﹣×2×4

＝4．