
【题目】如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

【答案】(1)(1,0);(2)①(4,21)或(﹣4,5);②当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.
【解析】试题分析:(1)由抛物线y=ax2+bx+c的对称轴为直线x=﹣1,交x轴于A、B两点,其中A点的坐标为(﹣3,0),根据二次函数的对称性,即可求得B点的坐标;
(2)①a=1时,先由对称轴为直线x=﹣1,求出b的值,再将B(1,0)代入,求出二次函数的解析式为y=x2+2x﹣3,得到C点坐标,然后设P点坐标为(x,x2+2x﹣3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
②先运用待定系数法求出直线AC的解析式为y=﹣x﹣3,再设Q点坐标为(x,﹣x﹣3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
试题解析:解:((1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称.
∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);
(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴ ![]() =﹣1,解得b=2.
=﹣1,解得b=2.
将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.
则二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3).∵S△POC=4S△BOC,∴ ![]() ×3×|x|=4×
×3×|x|=4×![]() ×3×1,∴|x|=4,x=±4.
×3×1,∴|x|=4,x=±4.
当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
②设直线AC的解析式为y=kx+t (k≠0)将A(﹣3,0),C(0,﹣3)代入,
得![]() ,解得
,解得![]() ,
,
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.



 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】甲和乙骑摩托车分别从某大道上相距6000米的A、B两地同时出发,相向而行,匀速行驶一段时间后,到达C地的甲发现摩托车出了故障,立即停下电话通知乙,乙接到电话后立即以出发时速度的![]() 倍向C地匀速骑行,到达C地后,用5分钟修好了甲摩托车,然后乙仍以出发时速度的
倍向C地匀速骑行,到达C地后,用5分钟修好了甲摩托车,然后乙仍以出发时速度的![]() 倍匀速向终点A地骑行,甲仍以原来速度向B地匀速骑行,2分钟后,发现乙的一件维修工具落在了自己车上,于是立即掉头并以原速度
倍匀速向终点A地骑行,甲仍以原来速度向B地匀速骑行,2分钟后,发现乙的一件维修工具落在了自己车上,于是立即掉头并以原速度![]() 倍的速度匀速返回(此时乙未到达A地).在这个过程中,两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(甲与乙打、接电话及掉头时间忽略不计)则当乙到达A地时,甲离A地的距离为 ________米.
倍的速度匀速返回(此时乙未到达A地).在这个过程中,两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(甲与乙打、接电话及掉头时间忽略不计)则当乙到达A地时,甲离A地的距离为 ________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径MN=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点M、N始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=4cm.

(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在圆相切时,如果半圆O与直线MN围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)运动员小涛的身高是1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,小涛跳离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )

A. 函数有最小值
B. 对称轴是直线x=![]()
C. 当x<![]() ,y随x的增大而减小
,y随x的增大而减小
D. 当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
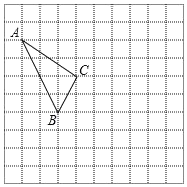
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,4),(﹣1,2).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)将△ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到△A′B′C′,画出平移后的△A′B′C′.
(3)求S△A′B′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com