练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（ ）

    A. 函数有最小值

    B. 对称轴是直线x=

    C. 当x＜，y随x的增大而减小

    D. 当﹣1＜x＜2时，y＞0

    【答案】D

    【解析】试题分析：根据抛物线的开口方向，利用二次函数的性质判断A；根据图形直接判断B；根据对称轴结合开口方向得出函数的增减性，进而判断C；根据图象，当-1＜x＜2时，抛物线落在x轴的下方，则y＜0，从而判断D．

    试题解析：A、由抛物线的开口向上，可知a＞0，函数有最小值，正确，故A选项不符合题意；

    B、由图象可知，对称轴为x=，正确，故B选项不符合题意；

    C、因为a＞0，所以，当x＜时，y随x的增大而减小，正确，故C选项不符合题意；

    D、由图象可知，当-1＜x＜2时，y＜0，错误，故D选项符合题意．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，下面的图象记录了某地一月份某大的温度随时间变化的情况，请你仔细观察图象回答下面的问题：

    （1）在这个问题中，变量分别是______，时间的取值范围是______；

    （2）20时的温度是______℃，温度是0℃的时刻是______时，最暖和的时刻是_______时，温度在－3℃以下的持续时间为______小时；

    （3）你从图象中还能获得哪些信息？（写出1～2条即可）

    答：__________________________________________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）每年的6月5日为世界环保日，为提倡低碳环保，某公司决定购买10台节省能源的新机器，现有甲、乙两种型号的新机器可选，其中每台的价格、工作量如下表．

    甲型机器

    乙型机器

    价格（万元/台）

    a

    b

    产量（吨/月）

    240

    180

    经调查：购买一台甲型机器比购买一台乙型机器多2万元，购买2台甲型机器比购买3台乙型机器少6万元．

    （1）求a、b的值；

    （2）若该公司购买新机器的资金不能超过110万元，请问该公司有几种购买方案？

    （3）在（2）的条件下，若公司要求每月的产量不低于2040吨，请你为该公司设计一种最省钱的购买方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．

    （1）求足球和篮球的单价各是多少元？

    （2）根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了加强建设“经济强、环境美、后劲足、群众富”的实力城镇，聚力脱贫攻坚，全面完成脱贫任务，某乡镇特制定一系列帮扶计划。现决定将A、B两种类型鱼苗共320箱运到某村养殖，其中A种鱼苗比B种鱼苗多80箱。

    （1）求A种鱼苗和B种鱼苗各多少箱？

    （2）现计划租用甲、乙两种货车共8辆，一次性将这批鱼苗全部运往同一目的地。已知甲种货车最多可装A种鱼苗40箱和B种鱼苗10箱，乙种货车最多可装A种鱼苗和B种鱼苗各20箱。如果甲种货车每辆需付运输费4000元，乙种货车每辆需付运输费3600元，则安排甲、乙两种货车有哪几种不同的方案？并说明选择哪种方案可使运输费最少？最少运输费是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元，小樱桃售价为每千克16元.

    (1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后，该水果商共赚了多少元钱?

    (2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知四边形ABCD中,∠ABC+∠ADC=180，连接AC，BD.

    (1)如图1,当∠ACD=∠CAD=45时，求∠CBD的度数；

    (2)如图2,当∠ACD=∠CAD=60时，求证：AB+BC=BD；

    (3)如图3,在(2)的条件下,过点C作CK⊥BD于点K,在AB的延长线上取点F,使∠FCG=60,过点F作FH⊥BD于点H,BD=8,AB=5,GK=，求BH的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

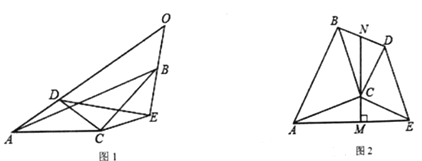
    【题目】在△ABC和△DCE中，CA=CB，CD=CE，∠CAB= ∠CED=α.

    (1)如图1，将AD、EB延长，延长线相交于点0.

    ①求证:BE= AD;

    ②用含α的式子表示∠AOB的度数(直接写出结果);

    (2)如图2,当α=45°时，连接BD、AE,作CM⊥AE于M点，延长MC与BD交于点N.求证:N是BD的中点.

    注:第(2)问的解答过程无需注明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（　　）

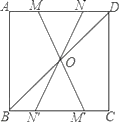
    A. 2对 B. 3对 C. 4对 D. 5对

    查看答案和解析>>

    同步练习册答案