
分析 根据题意画出图形,由点C(0,1)逆时针方向旋转90°刚好落在线AB得出其运动路径为线段E′E″,证Rt△E″E′C∽Rt△BAC可得$\frac{E′E″}{BA}$=$\frac{E′C}{AC}$,继而可得出答案.
解答 解:如图,由题意知点E的运动路径为线段E′E″,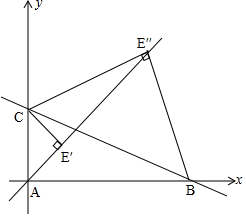
∵y=-$\frac{\sqrt{3}}{3}$x+1中,x=0时y=1,y=0时x=$\sqrt{3}$,
∴OC=1、OA=$\sqrt{3}$,
∴BC=2,
∵E′C=E′A、E″C=E″B,
∴E′C=$\frac{\sqrt{2}}{2}$、E″C=$\frac{\sqrt{2}}{2}$BC=$\sqrt{2}$,
则$\frac{E′C}{AC}$=$\frac{E″C}{BC}$=$\frac{\sqrt{2}}{2}$,
∴Rt△E″E′C∽Rt△BAC,
则$\frac{E′E″}{BA}$=$\frac{E′C}{AC}$,即$\frac{E′E″}{\sqrt{3}}$=$\frac{\sqrt{2}}{2}$,
∴E′E″=$\frac{\sqrt{6}}{2}$,
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题主要考查坐标与图形的变化及相似三角形的判定与性质,根据旋转的定义和性质得出点C的运动路径为线段E′E″及依据相似三角形的判定与性质得出其长度是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
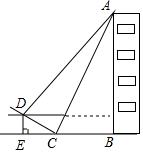 如图,我市某中学数学兴趣小组决定测量一下本校教学楼AB的高度,他们在楼梯底部C处测得∠ACB=60°,∠DCE=30°;沿楼梯向上走到D处测得∠ADF=45°,D到地面BE的距离DE为3米.求教学楼AB的高度.(站果精确列1米,参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7)
如图,我市某中学数学兴趣小组决定测量一下本校教学楼AB的高度,他们在楼梯底部C处测得∠ACB=60°,∠DCE=30°;沿楼梯向上走到D处测得∠ADF=45°,D到地面BE的距离DE为3米.求教学楼AB的高度.(站果精确列1米,参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
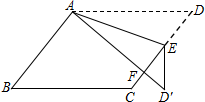 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )| A. | 20° | B. | 30° | C. | 36° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com