
【题目】如图,将ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED. 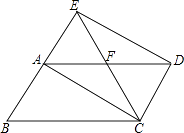
(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B,求证:四边形ACDE是矩形.
【答案】
(1)证明:∵ABCD中,AB=CD且AB∥CD,
又∵AE=CD,
∴AE=CD,AE∥CD,
∴四边形ACDE是平行四边形
(2)证明:∵ABCD中,AD∥BC,
∴∠EAF=∠B,
又∵∠AFC=∠EAF+∠AEF,∠AFC=2∠B
∴∠EAF=∠AEF,
∴AF=EF,
又∵平行四边形ACDE中AD=2AF,EC=2EF
∴AD=EC,
∴平行四边形ACDE是矩形
【解析】(1)证明AE=CD,AE∥CD,即可证得;(2)证明△AEF是等腰三角形,则可以证得AD=EC,根据对角线相等的平行四边形是矩形即可证得.
【考点精析】本题主要考查了平行四边形的判定与性质和矩形的判定方法的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】请你从下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC中任选两个,使它们能判定四边形ABCD是平行四边形.共有________种情况符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励城区居民节约用水,实行阶梯计价.规定用水收费标准如下:①每户每月的用水量不超过![]() 吨时,水费为
吨时,水费为![]() 元/吨时,不超过部分
元/吨时,不超过部分![]() 元/吨,超过部分为
元/吨,超过部分为![]() 元/吨.②收取污水处理费
元/吨.②收取污水处理费![]() 元/吨.
元/吨.
(![]() )若
)若![]() 用户四月份用水
用户四月份用水![]() 吨,应缴水费__________元.
吨,应缴水费__________元.
(![]() )若
)若![]() 用户五月份用水
用户五月份用水![]() 吨,缴水费
吨,缴水费![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,若
)的条件下,若![]() 用户某月共缴水费
用户某月共缴水费![]() 元,求该用户该月用水量.
元,求该用户该月用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将代数式4a2b+3ab2﹣2b2+a3按a的升幂排列的是( )
A.﹣2b3+3ab2+4a2b+a3
B.a3+4a2b+3ab2﹣2b3
C.4a2b+3ab2﹣2b3+a3
D.4a2b+3ab2+a3﹣2b3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题. 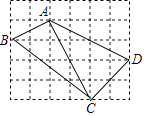
(1)线段AB的长为 , BC的长为 , CD的长为;
(2)连接AC,通过计算说明△ACD和△ABC是什么特殊三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com