
【题目】如图,在平面直角坐标系内,已知点A(0,6),点B(8,0).动点P从A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P,Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似,并求出此时点P的坐标.

【答案】(1)y=﹣![]() x+6;(2)当t为
x+6;(2)当t为![]() 秒或
秒或![]() 秒时,△APQ与△AOB相似
秒时,△APQ与△AOB相似
【解析】试题分析:(1)设直线AB的解析式为y=kx+b,解得k,b即可;
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t;②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
试题解析:解:(1)设直线AB的解析式为y=kx+b,由题意得:
![]() ,解得:
,解得: 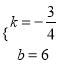 .
.
∴直线AB的解析式为y=﹣![]() x+6;
x+6;
(2)在Rt△AOB中,AO=6,BO=8,根据勾股定理得:AB=10.
由题意知:AP=t,AQ=10﹣2t.分两种情况讨论:
①当∠APQ=∠AOB时.∵∠A=∠A,∴△APQ∽△AOB,∴ ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
②当∠AQP=∠AOB时.∵∠A=∠A,∴△AQP∽△AOB,∴ ![]() ,∴t=
,∴t=![]() (秒).
(秒).
综上所述:当t为![]() 秒或
秒或![]() 秒时,△APQ与△AOB相似.
秒时,△APQ与△AOB相似.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 重合),过
重合),过![]() 作
作![]() ,垂足为
,垂足为![]() ,点
,点![]() 在边
在边![]() 上,且与点
上,且与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() .
.
(1)若![]() 平分
平分![]() ,求线
,求线![]() 的长;
的长;
(2)![]() 能否为等腰三角形?若能,请确定点
能否为等腰三角形?若能,请确定点![]() 的位置;若不能,请说明理由.
的位置;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
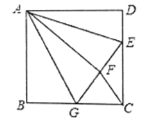
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG//CF;④S△EFC=![]() .其中正确结论的是____________(只填序号).
.其中正确结论的是____________(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课堂探究性活动蔚然成风。张老师在课堂上设置一道习题:
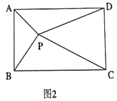
(1)已知矩形ABCD和点P,当点P在BC上任一位置(如图1所示)时,探究PA2、PB2、PC2、PD2,之间的关系?直接写出结论,不必证明;
当P点在其它位置时,请同学们分组探究:
(2)当点P在矩形内部,如图2时,探究PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论写出来,并给予证明。
(3)当点P在矩形外部,如图3时,继续探完PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论直接写出来,不必证明。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数
2 -4 8 -16 32 -64 ……
4 -2 10 -24 34 -62 ……
-1 5 -7 17 -31 65 ……
(1)第一行第7个数为
(2)第③行中是否存在连续的三个数使得三个数的和为768?若存在,求出这三个数;不存在,则说明理由;
(3)是否存在这样的一列,使得其中的三个数的和为1282?若存在,则求出这三个数,不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
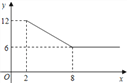
【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图;B类杨梅深加工后再销售,深加工总费用s(万元)与加工数量t(吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入﹣经营总成本)
(3)若该公司收购20吨杨梅,要使该公司获得30万元毛利润,求直销的A类杨梅有多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
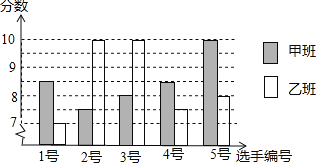
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com