
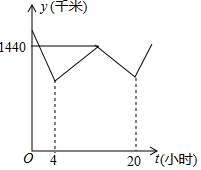
 甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.
甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米. 分析 设AC中点为E,根据乙车的运动速度不变结合函数图象,可得出AE=CE=2BC,进而可得出CE的长度,根据速度=路程÷时间即可求出甲、乙的运动速度,再根据两车之间的距离=两车速度和×掉头的时间,即可求出结论.
解答 解:设AC中点为E.
观察函数图象可知:乙车从B到C需用4小时,从C到E需用$\frac{20-4}{2}$=8小时,甲从A到E需要12小时,
∵点E为AC的中点,乙的速度不变,
∴AE=CE=2BC(如图所示).
∵2CE=1440,
∴AE=720,BE=1080,
∴甲的速度为720÷12=60(千米/小时),乙的速度为1080÷12=90(千米/小时).
第21小时时,甲乙两车之间的距离为(60+90)×(21-12)=1350(千米).
故答案为:1350.
点评 本题考查一次函数的应用,据乙车的运动结合函数图象,找出AE=CE=2BC是解题的关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:填空题
| 分数段(分) | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人数 | 1 | 3 | 4 | 8 | 13 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
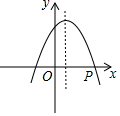 如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.
如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
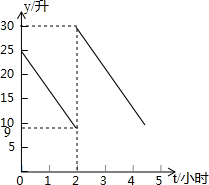 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(万元/件) | 100 | 80 |
| 售价(万元/件) | 170 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.
小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com