练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AD是高线，AE，BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°，求：

    （1）∠DAC的度数；

    （2）∠AOB的度数．

    【答案】(1)20°；（2）125°.

    【解析】试题分析：（1）因为AD是高，所以∠ADC=90°，又因为∠C=70°，所以∠DAC度数可求；

    （2）因为∠BAC=50°，∠C=70°，所以∠BAO=25°，∠ABC=60°，BF是∠ABC的角平分线，则∠ABO=30°，故∠BOA的度数可求．

    试题解析：（1）∵AD⊥BC，

    ∴∠ADC=90°，

    ∵∠C=70°，

    ∴∠DAC=180°﹣90°﹣70°=20°；

    （2）∵∠BAC=50°，∠C=70°，

    ∴∠BAO=25°，∠ABC=60°，

    ∵BF是∠ABC的角平分线，

    ∴∠ABO=30°，

    ∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一张矩形纸片，剪下一个正方形，剩下一个矩形，称为第一次操作；在剩下的矩形纸片中再剪下一个正方形，剩下一个矩形，称为第二次操作；…；若在第n次操作后，剩下的矩形为正方形，则称原矩形为n阶奇异矩形．

    （1）如图1，矩形ABCD中，若AB=3，BC=9，则称矩形ABCD为　　阶奇异矩形．

    （2）如图2，矩形ABCD长为7，宽为3，它是奇异矩形吗？如果是，请写出它是几阶奇异矩形，并在图中画出裁剪线；如果不是，请说明理由．

    （3）已知矩形ABCD的一边长为20，另一边长为a（a＜20），且它是3阶奇异矩形，请画出矩形ABCD及裁剪线的示意图，并在图的下方直接写出a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x，y的多项式xy -5x+mxy +y-1不含二次项，则m的值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列调查中，适宜采用普查方式的是（ ）

    A.调查银川市市民垃圾分类的情况B.对市场上的冰淇淋质量的调查

    C.对乘坐某次航班的乘客进行安全检查D.对全国中学生心理健康现状的调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是O的直径，点C在O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.

    (1)求证：PC是O的切线；

    (2)求证： ；

    (3)点M是弧AB的中点，CM交AB于点N，若AB=4，求MN·MC的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】水果市场将120吨水果运往各地商家，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：(假设每辆车均满载)

    车型

    甲

    乙

    丙

    汽车运载量(吨/辆)

    5

    8

    10

    汽车运费(元/辆)

    400

    500

    600

    （1）若全部水果都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

    （2）为了节约运费，市场可以调用甲、乙、丙三种车型参与运送（每种车型至少1辆），已知它们的总辆数为16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线经过O，D，C三点.

    (1)求AD的长及抛物线的解析式；

    (2)一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动，设运动时间为t秒，当t为何值时，以P，Q，C为顶点的三角形与△ADE相似？

    (3)点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:如图,A、B、C、D 为矩形的四个顶点,AB＝16cm，AD＝

    6cm，动点P、Q 分别从A、C 同时出发,点P 以3cm/s的速度向点B 移动,

    一直到达点 B 为止,点 Q 以2cm/s的速度向点 D 移动．

    （1）P、Q 两点从出发点出发几秒时,四边形PBCQ 的面积是33cm2?

    （2）P、Q 两点从出发点出发几秒时,点P、Q 间的距离是10cm?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为a的正方形ABCD和边长为b（a＞b）的正方形CEFG拼在一起，B、C、E三点在同一直线上，设图中阴影部分的面积为S.

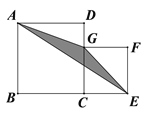
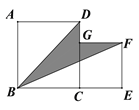
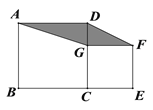
    图① 图② 图③

    （1）如图①，S的值与a的大小有关吗？说明理由；

    （2）如图②，若a＋b＝10，ab＝21，求S的值；

    （3）如图③，若a－b＝2，＝7，求的值.

    查看答案和解析>>

    同步练习册答案