
����Ŀ��һ�ž���ֽƬ������һ�������Σ�ʣ��һ�����Σ���Ϊ��һ�β�������ʣ�µľ���ֽƬ���ټ���һ�������Σ�ʣ��һ�����Σ���Ϊ�ڶ��β������������ڵ�n�β�����ʣ�µľ���Ϊ�����Σ����ԭ����Ϊn��������Σ�
��1����ͼ1������ABCD�У���AB=3��BC=9����ƾ���ABCDΪ������������Σ�
��2����ͼ2������ABCD��Ϊ7����Ϊ3�������������������ǣ���д�����Ǽ���������Σ�����ͼ�л����ü��ߣ�������ǣ���˵�����ɣ�
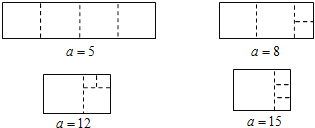
��3����֪����ABCD��һ�߳�Ϊ20����һ�߳�Ϊa��a��20����������3��������Σ��뻭������ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�ֱ��д��a��ֵ��

���𰸡���1��2 ��2������ABCD��4��������� ��3��ͼ�μ�����
�������������������1����֪����2�β�����ʣ�µľ���Ϊ�����Σ� ���Ծ���ABCDΪ2���������. ��1��������֪�������軭�����ɣ���2��������֪�ó�������������4�����������ͼ�μ��ɣ�
�⣺��1������2�β�����ʣ�µľ���Ϊ�����Σ�
�� ����ABCDΪ2���������
��2������ABCD��4��������Σ��ü��ߵ�ʾ��ͼ���£�

��3���ü��ߵ�ʾ��ͼ���£�


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�У��������a5���ǣ�������
A. a2+a3 B. a2a3 C. a5��a D. ��a2��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������̳����ж�������ijһ��Ʒ��
��1�����̳�������Ʒ���15%����ۼ�Ϊ1.15Ԫ�������Ʒ�ڼ��̳���ԭ��Ϊ �� Ԫ��
��2�����̳�������Ʒ���20%����6ԪǮ�������Ʒ�ļ�����û���ǰ����1���������Ʒ�����̳���ԭ���Ƕ��٣�
��3���ڣ�1������2��С��������£��ס������̳��Ѹ���Ʒ����ԭ�۽��������μ۸������
���̳�����һ����۵İٷ�����![]() ���ڶ�����۵İٷ�����
���ڶ�����۵İٷ�����![]() ��
��
���̳���������۵İٷ��ʶ���![]() (
(![]() ��
��
���ʼס������̳����ĸ��̳�����۽϶ࣿ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������
��1����֤��AB��CD��
��2����ͼ2����AEF���EFC�Ľ�ƽ�����ཻ�ڵ�P��ֱ��EP��ֱ��CD���ڵ�G������G��EG�Ĵ��ߣ���ֱ��MN�ڵ�H����֤��PF��GH��
��3����ͼ3���ڣ�2���������£�����PH��K��GH��һ�㣬�ҡ�PHK=��HPK������EPK��ƽ���߽�ֱ��MN�ڵ�Q���ʡ�HPQ�Ĵ�С�Ƿ����仯�������䣬�������HPQ�Ķ��������仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�տ����������һ���Ϊ����ABCD��С�ݣ�AB+BC=10m��˩סС����10m��������һ�˹̶���B�㴦��С���ڲ��ܽ���С���ڵ������»������Ի���������ΪS��m2����
��1����ͼ1����BC=4m����S=_______m2��
��2����ͼ2���ֿ����ڣ�1���еľ���ABCDС�ݵ��Ҳ���CDΪ����չһ����CDE����ʹ֮������Ϊ�����ABCED��С�ݣ������������䣬����BC�ı仯�����У���Sȡ����Сֵʱ����BC�ij�Ϊ________m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���ͼ����֪������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C������BC�������ߵĶԳ����ڵ�E��D�������ߵĶ��㣮
��1����������ߵĽ���ʽ��
��2��ֱ��д����C�͵�D�����ꣻ
��3������P�ڵ�һ�����ڵ��������ϣ���S��ABP=4S��COE����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD�Ǹ��ߣ�AE��BF�ǽ�ƽ���ߣ������ཻ�ڵ�O����BAC=50������C=70������
��1����DAC�Ķ�����
��2����AOB�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com