
¡ŸÌâÄ¿¡¿ÔÚÒ»¿Õ¿õ³¡µØÉÏÉèŒÆÒ»ÂäµØΪŸØÐÎABCDµÄСÎÝ£¬AB+BC=10m£¬Ë©×¡Ð¡¹·µÄ10m³€µÄÉþ×ÓÒ»¶Ë¹Ì¶šÔÚBµãŽŠ£¬Ð¡¹·ÔÚ²»ÄÜœøÈëСÎÝÄÚµÄÌõŒþÏ»£¬Æä¿ÉÒԻµÄÇøÓòÃæ»ýΪS£šm2£©£®
£š1£©ÈçÍŒ1£¬ÈôBC=4m£¬ÔòS=_______m2£®
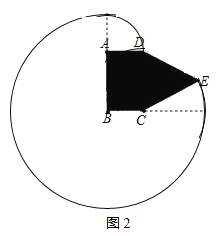
£š2£©ÈçÍŒ2£¬ÏÖ¿ŒÂÇÔÚ£š1£©ÖеğØÐÎABCDСÎݵÄÓÒ²àÒÔCDΪ±ßÍØÕ¹Ò»Õý¡÷CDEÇøÓò£¬Ê¹Ö®±ä³ÉÂäµØΪÎå±ßÐÎABCEDµÄСÎÝ£¬ÆäËûÌõŒþ²»±ä£¬ÔòÔÚBCµÄ±ä»¯¹ý³ÌÖУ¬µ±SÈ¡µÃ×îСֵʱ£¬±ßBCµÄ³€Îª________m£®

¡ŸŽð°ž¡¿ 88ŠÐ ![]()
¡ŸœâÎö¡¿œâ£º£š1£©ÈçÍŒ1£¬Ë©×¡Ð¡¹·µÄ10m³€µÄÉþ×ÓÒ»¶Ë¹Ì¶šÔÚBµãŽŠ£¬Ð¡¹·¿ÉÒԻµÄÇøÓòÈçÍŒËùÊŸ£º
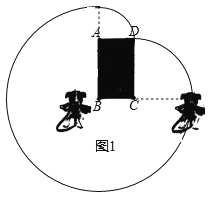
ÓÉÍŒ¿ÉÖª£¬Ð¡¹·»î¶¯µÄÇøÓòÃæ»ýΪÒÔBΪԲÐÄ¡¢10Ϊ°ëŸ¶µÄ![]() Ô²£¬ÒÔCΪԲÐÄ¡¢6Ϊ°ëŸ¶µÄ
Ô²£¬ÒÔCΪԲÐÄ¡¢6Ϊ°ëŸ¶µÄ![]() Ô²ºÍÒÔAΪԲÐÄ¡¢4Ϊ°ëŸ¶µÄ
Ô²ºÍÒÔAΪԲÐÄ¡¢4Ϊ°ëŸ¶µÄ![]() Ô²µÄÃæ»ýºÍ£¬¡àS=
Ô²µÄÃæ»ýºÍ£¬¡àS=![]() ¡ÁŠÐ102+
¡ÁŠÐ102+![]() ŠÐ62+
ŠÐ62+![]() ŠÐ42=88ŠÐ£»
ŠÐ42=88ŠÐ£»
£š2£©ÈçÍŒ2£¬ÉèBC=x£¬ÔòAB=10©x£¬¡àS=![]() ŠÐ102+
ŠÐ102+![]() ŠÐx2+
ŠÐx2+![]() ŠÐ£š10©x£©2
ŠÐ£š10©x£©2
=![]() £šx2©10x+250£©=
£šx2©10x+250£©=![]() £šx2©5x+250£©£¬µ±x=
£šx2©5x+250£©£¬µ±x=![]() ʱ£¬SÈ¡µÃ×îСֵ£¬¡àBC=
ʱ£¬SÈ¡µÃ×îСֵ£¬¡àBC=![]() £®
£®
¹ÊŽð°žÎª£º88ŠÐ£» ![]() £®
£®



| Äꌶ | žßÖÐ¿Î³Ì | Äꌶ | ³õÖÐ¿Î³Ì |
| žßÒ» | žßÒ»Ãâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍÆŒö£¡ |
| žß¶þ | žß¶þÃâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍÆŒö£¡ |
| žßÈý | žßÈýÃâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍÆŒö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬Å×ÎïÏßy=©x2+bx+cÓëxÖá·Ö±ðœ»ÓÚA£š©1£¬0£©£¬B£š5£¬0£©Áœµã£®
£š1£©ÇóÅ×ÎïÏߵĜâÎöÊœ£»
£š2£©ÔÚµÚ¶þÏóÏÞÄÚÈ¡Ò»µãC£¬×÷CDŽ¹Ö±XÖáÓÚµãD£¬ÁŽœÓAC£¬ÇÒAD=5£¬CD=8£¬œ«Rt¡÷ACDÑØxÖáÏòÓÒÆœÒÆmžöµ¥Î»£¬µ±µãCÂäÔÚÅ×ÎïÏßÉÏʱ£¬ÇómµÄÖµ£»
£š3£©ÔÚ£š2£©µÄÌõŒþÏ£¬µ±µãCµÚÒ»ŽÎÂäÔÚÅ×ÎïÏßÉÏŒÇΪµãE£¬µãPÊÇÅ×ÎïÏ߶ԳÆÖáÉÏÒ»µã£®ÊÔÌœŸ¿£ºÔÚÅ×ÎïÏßÉÏÊÇ·ñŽæÔÚµãQ£¬Ê¹ÒÔµãB¡¢E¡¢P¡¢QΪ¶¥µãµÄËıßÐÎÊÇÆœÐÐËıßÐΣ¿ÈôŽæÔÚ£¬Çë³öµãQµÄ×ø±ê£»Èô²»ŽæÔÚ£¬Çë˵Ã÷ÀíÓÉ£®

²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÇëÐŽ³öÒ»žöÂú×ãÏÂÁÐÌõŒþµÄ¶þŽÎÈýÏîÊœ_____£¬žÃ¶àÏîʜֻº¬ÓÐ×ÖÄžx£¬¶þŽÎÏîϵÊýÊÇ1£¬Ò»ŽÎÏîϵÊýÊÇ©2£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿Ò»ÕÅŸØÐÎ֜Ƭ£¬ŒôÏÂÒ»žöÕý·œÐΣ¬Ê£ÏÂÒ»žöŸØÐΣ¬³ÆΪµÚÒ»ŽÎ²Ù×÷£»ÔÚʣϵğØÐÎ֜ƬÖÐÔÙŒôÏÂÒ»žöÕý·œÐΣ¬Ê£ÏÂÒ»žöŸØÐΣ¬³ÆΪµÚ¶þŽÎ²Ù×÷£»¡£»ÈôÔÚµÚnŽÎ²Ù×÷ºó£¬Ê£ÏµğØÐÎΪÕý·œÐΣ¬Ôò³ÆÔŸØÐÎΪnœ×ÆæÒìŸØÐΣ®
£š1£©ÈçÍŒ1£¬ŸØÐÎABCDÖУ¬ÈôAB=3£¬BC=9£¬Ôò³ÆŸØÐÎABCDΪ¡¡¡¡œ×ÆæÒìŸØÐΣ®
£š2£©ÈçÍŒ2£¬ŸØÐÎABCD³€Îª7£¬¿íΪ3£¬ËüÊÇÆæÒìŸØÐÎÂð£¿Èç¹ûÊÇ£¬ÇëÐŽ³öËüÊÇŒžœ×ÆæÒìŸØÐΣ¬²¢ÔÚÍŒÖл³ö²ÃŒôÏߣ»Èç¹û²»ÊÇ£¬Çë˵Ã÷ÀíÓÉ£®
£š3£©ÒÑÖªŸØÐÎABCDµÄÒ»±ß³€Îª20£¬ÁíÒ»±ß³€Îªa£ša£Œ20£©£¬ÇÒËüÊÇ3œ×ÆæÒìŸØÐΣ¬Ç뻳öŸØÐÎABCDŒ°²ÃŒôÏßµÄÊŸÒâÍŒ£¬²¢ÔÚÍŒµÄÏ·œÖ±œÓÐŽ³öaµÄÖµ£®

²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
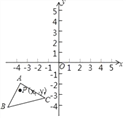
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬¡÷A¡äB¡äC¡äÊÇ¡÷ABCŸ¹ýÆœÒƵõœµÄ£¬¡÷ABCÈýžö¶¥µãµÄ×ø±ê·Ö±ðΪA£š©4£¬©1£©£¬B£š©5£¬©4£©£¬C£š©1£¬©3£©£¬¡÷ABCÖÐÈÎÒâÒ»µãP£šx1£¬y1£©ÆœÒƺóµÄ¶ÔÓŠµãΪP¡ä£šx1+6£¬y1+4£©
£š1£©ÇëÐŽ³öÈýœÇÐÎABCÆœÒƵĹý³Ì£»
£š2£©ÐŽ³öµãA¡ä£¬C¡äµÄ×ø±ê£»
£š3£©Çó¡÷A¡äB¡äC¡äµÄÃæ»ý£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªAM¡ÎCN£¬µãBΪƜÃæÄÚÒ»µã£¬AB¡ÍBCÓÚB£®
£š1£©ÈçÍŒ1£¬Ö±œÓÐŽ³ö¡ÏAºÍ¡ÏCÖ®ŒäµÄÊýÁ¿¹Øϵ________£»
£š2£©ÈçÍŒ2£¬¹ýµãB×÷BD¡ÍAMÓÚµãD£¬ÇóÖ€£º¡ÏABD=¡ÏC£»
£š3£©ÈçÍŒ3£¬ÔÚ£š2£©ÎʵÄÌõŒþÏ£¬µãE¡¢FÔÚDMÉÏ£¬Á¬œÓBE¡¢BF¡¢CF£¬BFÆœ·Ö¡ÏDBC£¬BEÆœ·Ö¡ÏABD£¬Èô¡ÏFCB+¡ÏNCF=180¡ã£¬¡ÏBFC=3¡ÏDBE£¬Çó¡ÏEBCµÄ¶ÈÊý£®

²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿œüËÆÊý2.30¡Á104µÄŸ«È·¶ÈÊÇ______£¬œ«2019Ÿ«È·µœÊ®Î»µÄœá¹ûÊÇ______£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿Ë®¹ûÊг¡œ«120¶ÖË®¹ûÔËÍùž÷µØÉ̌ң¬ÏÖÓЌס¢ÒÒ¡¢±ûÈýÖÖ³µÐ͹©Ñ¡Ôñ£¬Ã¿ÁŸ³µµÄÔËÔØÄÜÁŠºÍÔË·ÑÈçϱíËùÊŸ£º(ŒÙÉèÿÁŸ³µŸùÂúÔØ)
³µÐÍ | Œ× | ÒÒ | ±û |
Æû³µÔËÔØÁ¿(¶Ö/ÁŸ) | 5 | 8 | 10 |
Æû³µÔË·Ñ(Ôª/ÁŸ) | 400 | 500 | 600 |
£š1£©ÈôÈ«²¿Ë®¹û¶ŒÓÌס¢ÒÒÁœÖÖ³µÐÍÀŽÔËËÍ£¬ÐèÔË·Ñ8200Ôª£¬ÎÊ·Ö±ðÐèŒ×¡¢ÒÒÁœÖÖ³µÐÍž÷ŒžÁŸ£¿
£š2£©ÎªÁËœÚÔŒÔË·Ñ£¬Êг¡¿ÉÒÔµ÷ÓÌס¢ÒÒ¡¢±ûÈýÖÖ³µÐͲÎÓëÔËËÍ£šÃ¿ÖÖ³µÐÍÖÁÉÙ1ÁŸ£©£¬ÒÑÖªËüÃǵÄ×ÜÁŸÊýΪ16ÁŸ£¬ÄãÄÜÍš¹ýÁзœ³Ì×éµÄ·œ·š·Ö±ðÇó³öŒžÖÖ³µÐ͵ÄÁŸÊýÂð£¿
²é¿ŽŽð°žºÍœâÎö>>
¹úŒÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·šºÍ²»ÁŒÐÅÏ¢ŸÙ±šÆœÌš | ÍøÉÏÓкŠÐÅÏ¢ŸÙ±š×šÇø | µçÐÅÕ©ÆŸÙ±š×šÇø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓкŠÐÅÏ¢ŸÙ±š×šÇø | ÉæÆóÇÖÈšŸÙ±š×šÇø
Î¥·šºÍ²»ÁŒÐÅÏ¢ŸÙ±šµç»°£º027-86699610 ŸÙ±šÓÊÏ䣺58377363@163.com