
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 26、
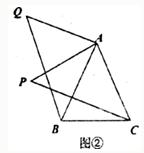
26、 复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| PG |
| PC |
| PG |
| PC |
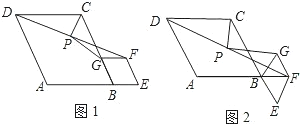 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出| PG |
| PC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 17、如图(1)已知在△ABC中,AB=AC,P是△ABC内任意一点将AP绕点A顺时针旋转到AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP,请证明;
17、如图(1)已知在△ABC中,AB=AC,P是△ABC内任意一点将AP绕点A顺时针旋转到AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP,请证明;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图(1)已知在△ABC中,AB=AC,P是△ABC内任意一点将AP绕点A顺时针旋转到AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP,请证明;
如图(1)已知在△ABC中,AB=AC,P是△ABC内任意一点将AP绕点A顺时针旋转到AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP,请证明;查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(48)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com