

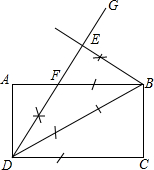
 解:(1)做法参考:
解:(1)做法参考:| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、② | B、②④ | C、②③ | D、①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、30 | B、40 | C、45 | D、50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知电流在一定时间内正常通过电子元件的概率为0.5,分别求在一定时间内A、B之间电流通过的概率.(要求:解答分两步:第一步用列举法写出各种可能的结果;第二步,求A、B之间电流通过的概率.)
已知电流在一定时间内正常通过电子元件的概率为0.5,分别求在一定时间内A、B之间电流通过的概率.(要求:解答分两步:第一步用列举法写出各种可能的结果;第二步,求A、B之间电流通过的概率.)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知一次函数y=kx+b与y=mx+n的图象如图所示.
已知一次函数y=kx+b与y=mx+n的图象如图所示.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com