
 如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)
如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号) 分析 ①根据有两组对应角相等的三角形相似即可证明.
②根据只有一组对应角相等且的两三角形不一定相似,即可证得.
③分两种情况讨论,通过三角形相似即可求得.
④依据相似三角形对应边成比例即可求得.
解答 解:①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADC=180°-α-∠BDE,
∵∠BED=180°-α-∠BDE,
∴∠BED=∠ADC
∴△DBE∽△ACD,故①正确;
②∵∠B=∠C,
∴∠C=∠ADE,
不能得到△ADE∽△ACD;
故②错误,
③当∠AED=90°时,由①可知:△ADE∽△ABD,
∴∠ADB=∠AED,
∵∠AED=90°,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α且cosα=$\frac{4}{5}$,AB=10,
BD=8.
当∠BDE=90°时,易△BDE∽△CAD,
∵∠BDE=90°,
∴∠CAD=90°,
∵∠B=α且cosα=$\frac{4}{5}$.AB=10,
∴cosC=$\frac{AC}{CD}$=$\frac{4}{5}$,
∴CD=$\frac{25}{2}$,
∴BD=BC-CD=$\frac{7}{2}$;
故③正确.
④过A作AG⊥BC于G,∵cosα=$\frac{4}{5}$,
∴BG=8,
∴BC=16,易证得△BDE∽△CAD,
设BD=y,BE=x,
∴$\frac{AB}{DE}$=$\frac{CD}{BE}$,
∴$\frac{10}{16-y}$=$\frac{y}{x}$,
整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,
∴0<x≤6.4.
故④错误.
故答案为:①③.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质以及利用三角函数求边长等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
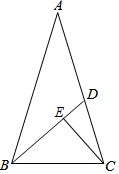 如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )
如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}+3}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
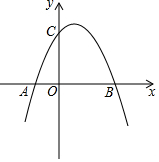 如图,已知抛物线y=-x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.
如图,已知抛物线y=-x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知BD是⊙O的直径,点A、C均在⊙O上,连接AO、DC,若$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则圆周角∠BDC的大小是( )
如图,已知BD是⊙O的直径,点A、C均在⊙O上,连接AO、DC,若$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则圆周角∠BDC的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
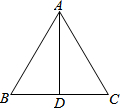 如图,下列条件不能推出△ABC是等腰三角形的是( )
如图,下列条件不能推出△ABC是等腰三角形的是( )| A. | ∠B=∠C | B. | AD⊥BC,∠BAD=∠CAD | C. | AD⊥BC,∠BAD=∠ACD | D. | AD⊥BC,BD=CD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
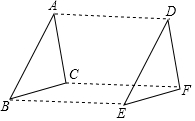 如图,△DEF是由△ABC平移得到的,对于结论:①BC=EF;②AB∥DE;③△ABC≌△DEF;④四边形ACFD为平行四边形,正确的是( )
如图,△DEF是由△ABC平移得到的,对于结论:①BC=EF;②AB∥DE;③△ABC≌△DEF;④四边形ACFD为平行四边形,正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com