


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
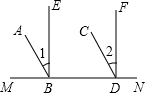
 (2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)
(2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省金华四中九年级毕业生学业考试模拟数学卷(带解析) 题型:解答题
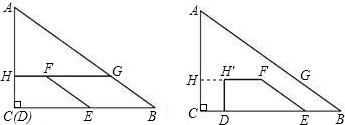
如图1,在等腰梯形ABCO中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A,B在第一象限内.
(1)求点E的坐标及线段AB的长;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,连结PN,设PE=x.△PMN的面积为S.
①求S关于x的函数关系式;
②△PMN的面积是否存在最大值,若不存在,请说明理由.若存在,求出面积的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2).设运动时间为t秒,运动后的直角梯形为E′D′G′H′(如图3);试探究:在运动过程中,等腰梯ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2012届浙江省九年级毕业生学业考试模拟数学卷(解析版) 题型:解答题
如图1,在等腰梯形ABCO中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A,B在第一象限内.
(1)求点E的坐标及线段AB的长;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,连结PN,设PE=x.△PMN的面积为S.
①求S关于x的函数关系式;
②△PMN的面积是否存在最大值,若不存在,请说明理由.若存在,求出面积的最大值;
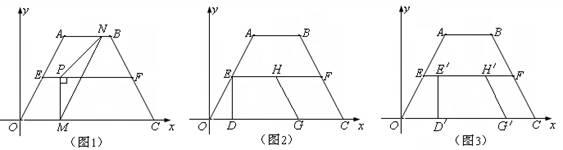
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2).设运动时间为t秒,运动后的直角梯形为E′D′G′H′(如图3);试探究:在运动过程中,等腰梯ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com