
 如图,一艘轮船在A处测得北偏东45°方向有一灯塔B,船向正东方向航行到达C处时,又观测到灯塔B在北偏东30°方向上,此时轮船与灯塔相距60海里,求轮船从A处到C处航行了多少海里(结果保留根号).
如图,一艘轮船在A处测得北偏东45°方向有一灯塔B,船向正东方向航行到达C处时,又观测到灯塔B在北偏东30°方向上,此时轮船与灯塔相距60海里,求轮船从A处到C处航行了多少海里(结果保留根号). 分析 作BD⊥AC交AC的延长线于D,根据正弦和余弦的定义分别求出CD、BD的长,根据直角三角形的性质求出AD的长,计算即可.
解答 解: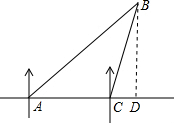 作BD⊥AC交AC的延长线于D,
作BD⊥AC交AC的延长线于D,
在Rt△BCD中,∠CBD=30°,
∴CD=$\frac{1}{2}$BC=30,
BD=BC•cos∠CBD=30$\sqrt{3}$,
∵∠BAD=45°,
∴AD=BD=30$\sqrt{3}$,
∴AC=30$\sqrt{3}$-30(海里),
答:轮船从A处到C处航行了(30$\sqrt{3}$-30)海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的概念是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 出现正面的频率是4 | B. | 出现反面的频率是6 | ||
| C. | 出现反面的频数是60% | D. | 出现反面的频率是60% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,现准备把坡角降为∠CAD=15°.
如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,现准备把坡角降为∠CAD=15°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5<a≤6 | B. | 4<a≤5 | C. | 4≤a<5 | D. | 5≤a<6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,则∠AOF的度数为( )
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,则∠AOF的度数为( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com