
 如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.分析 (1)欲证明DE是⊙O的切线,只要证明AC⊥OD,ED⊥OD即可.
(2)由△AFO≌△CFD(SAS),推出S△AFO=S△CFD,推出S四边形ACDE=S△ODE,求出△ODE的面积即可.
解答 (1)证明:∵D为$\widehat{AC}$的中点,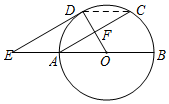 ∴OD⊥AC,
∴OD⊥AC,
∵AC∥DE,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接DC,
∵D为$\widehat{AC}$的中点,
∴OD⊥AC,AF=CF,
∵AC∥DE,且OA=AE,
∴F为OD的中点,即OF=FD,
在△AFO和△CFD中,
$\left\{\begin{array}{l}{AF=CF}\\{∠AFO=∠CFD}\\{OF=FD}\end{array}\right.$
∴△AFO≌△CFD(SAS),
∴S△AFO=S△CFD,
∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=4,
∴OE=8,
∴DE=$\sqrt{O{E}^{2}-O{D}^{2}}$=4$\sqrt{3}$,
∴S四边形ACDE=S△ODE=$\frac{1}{2}$×OD×DE=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$.
点评 本题考查切线的判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 540元 | B. | 1080元 | C. | 1620元 | D. | 1800元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
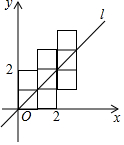 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$.
如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{2+a}$=$\frac{1}{1+a}$ | B. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | C. | $\frac{-x+y}{x-y}$=$\frac{x+y}{y-x}$ | D. | $\frac{{a}^{2}-1}{a+1}$=a-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com