
【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF. 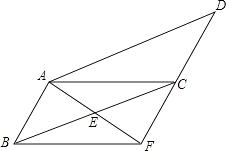
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAF=∠CFA.
∵E为BC的中点,
∴BE=CE.
在△AEB和△FEC中,
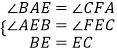 ,
,
∴△AEB≌△FEC(AAS)
∴AB=CF
(2)解:当BC=AF时,四边形ABFC是矩形,
理由:∵AB=CF,AB‖CF,
∴四边形ABFC是平行四边形,
∵BC=AF,
∴四边形ABFC是矩形.
【解析】(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;(2)首先得出四边形ABFC是平行四边形,进而得出答案.
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形即可以解答此题.


科目:初中数学 来源: 题型:
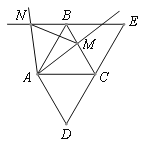
【题目】已知,如图,将∠D=60°的菱形ABCD沿对角线AC剪开,将△ADC沿射线DC方向平移,得到△BCE. 点M为BC边上一点(点M不与点B、点C重合),将射线AM绕点A逆时针旋转60°,与EB的延长线交于点N,连接MN.
(1)求证:∠ANB=∠AMC;
(2)探究△AMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD·OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2, ![]() .
.
①求⊙O的半径;②求sin∠BAD的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)填空: 31﹣30=2×3( ) ,
32﹣31=2×3( ) ,
33﹣32=2×3( ) ,
…
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;
(3)计算30+31+32+…+32016 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB= ![]() ,则此三角形移动的距离AA′是( )
,则此三角形移动的距离AA′是( ) 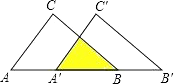
A.![]() ﹣1
﹣1
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年省政府工作报告中提到:“脱贫攻坚连战连捷.预计18个贫困县摘帽,725个贫困村出列、72.6万贫困人口脱贫的年度目标如期实现”.其中72.6万用科学记数法表示为( )
A. 72.6×104B. 7.26×105C. 7.26×106D. 72.6×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菏泽市大力推功新旧动能转换,产业转型升级迈出新步伐.建立了新旧动能转换项目,筛选论证项目325个,计划总投资3137亿元,3137亿用科学记数法表示为( )
A. 0.3137×1012B. 3.137×1012
C. 3.137×1011D. 3137×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是三角形纸片ABC的高,将纸片沿直线EF折叠,使点A与点D重合,给出下列判断: ①EF是△ABC的中位线;
②△DEF的周长等于△ABC周长的一半;
③若四边形AEDF是菱形,则AB=AC;
④若∠BAC是直角,则四边形AEDF是矩形,
其中正确的是( )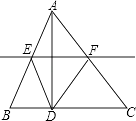
A.①②③
B.①②④
C.②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
(1)填空:∠ABC= , BC= .
(2)若点A在网格所在的坐标平面里的坐标为(1,﹣2),请你在图中找出一点D,写出以A、B、C、D四个点为顶点的四边形是平行四边形,在图中标出满足条件的D点位置,并直接写出D点坐标. 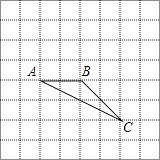
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com