
【题目】根据题意解答
(1)填空: 31﹣30=2×3( ) ,
32﹣31=2×3( ) ,
33﹣32=2×3( ) ,
…
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;
(3)计算30+31+32+…+32016 .
【答案】
(1)解:31﹣30=2×30,32﹣31=2×31,33﹣32=2×32
(2)解:规律:3n﹣3n﹣1=2×3n﹣1,
证明:3n﹣3n﹣1=3×3n﹣1﹣1×3n﹣1=2×3n﹣1
(3)解:设S=3°+31+32+33+…+32015+32016,
则3S=31+32+33+…+32015+32017,
所以2S=(31+32+33+…+32015+32017)﹣(30+31+32+33+…+32015+32016)=32017﹣1,
S= ![]() (32017﹣1)
(32017﹣1)
【解析】(1)根据有理数的乘方的定义进行计算即可得解;(2)根据指数结果幂的指数比等式的序数小1解答;(3)设S=3°+31+32+33+…+32015+32016 , 然后表示出3S,再相减计算即可得解.
【考点精析】根据题目的已知条件,利用有理数的乘方的相关知识可以得到问题的答案,需要掌握有理数乘方的法则:1、正数的任何次幂都是正数2、负数的奇次幂是负数;负数的偶次幂是正数;注意:当n为正奇数时: (-a)n=-an或(a -b)n=-(b-a)n , 当n为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n.


科目:初中数学 来源: 题型:
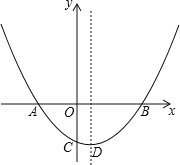
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)若点M为抛物线第四象限内一点,连接BC、CM、BM,求当△BCM的面积最大时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF. 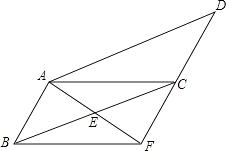
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com