
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)若点M为抛物线第四象限内一点,连接BC、CM、BM,求当△BCM的面积最大时点M的坐标.
【答案】(1)抛物线解析式为y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,抛物线的顶点坐标为(
,抛物线的顶点坐标为(![]() ,﹣
,﹣![]() ),(3)点M的坐标为(1,-1).
),(3)点M的坐标为(1,-1).
【解析】试题分析:(1)利用待定系数法求出抛物线解析式;
(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可.
(3)作出辅助线,利用tan∠MDN=2或![]() ,建立关于点N的横坐标的方程,求出即可.
,建立关于点N的横坐标的方程,求出即可.
试题解析:(1)∵抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,
∴![]()
∴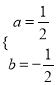 ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣1=
x﹣1=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴抛物线的顶点坐标为(![]() ,﹣
,﹣![]() ),
),
(2)如图1,
连接BC与抛物线对称轴的交点就是点P,连接AC,AP,
∵点A,B关于抛物线对称轴对称,
∴PA=PB,
∵B(2,0),C(0,﹣1),
∴直线BC解析式为y=![]() x﹣1,
x﹣1,
∵点P在抛物线对称轴上,
∴点P的横坐标为![]() ,
,
∴点P的纵坐标为﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() ),
),
(3)设M(x, ![]() ),过点M作x轴的垂线交BC于点N,则点N(x,
),过点M作x轴的垂线交BC于点N,则点N(x, ![]() )
)
∴![]() =
=![]() =
=![]()
故当x=1时,S△BMC面积最大,此时![]() ,
,
所以当△BCM的面积最大时点M的坐标为(1,-1).


科目:初中数学 来源: 题型:
【题目】数轴上点A和点B表示的教分别为﹣4和2,把点A向右平移( )个单位长度,可以使点A到点B的距离是2.
A. 2或4 B. 4或6 C. 6或8 D. 4或8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0). 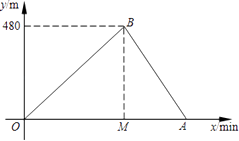
(1)A点所表示的实际意义是; ![]() =;
=;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于投针实验的说法正确的是( )
A. 针与平行线相交和不相交的可能性是相同的
B. 针与平行线相交的概率与针的长度没有关系
C. 实验次数越多,估算针与平行线相交的概率越精确
D. 针与平行线相交的概率不受两平行线间距离的影响
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是; 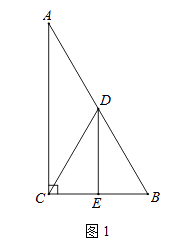
(2)如图2,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论; 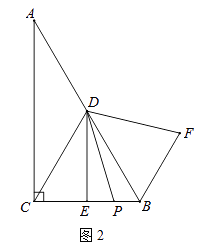
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系. 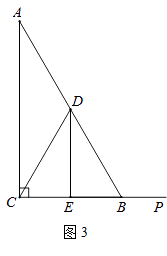
查看答案和解析>>
科目:初中数学 来源: 题型:
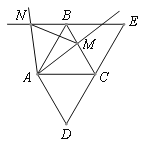
【题目】已知,如图,将∠D=60°的菱形ABCD沿对角线AC剪开,将△ADC沿射线DC方向平移,得到△BCE. 点M为BC边上一点(点M不与点B、点C重合),将射线AM绕点A逆时针旋转60°,与EB的延长线交于点N,连接MN.
(1)求证:∠ANB=∠AMC;
(2)探究△AMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列各数:2,﹣3,﹣0.56,﹣11,35,0.618,﹣125,+2.5,﹣136,﹣2.333,0,其中负数有( )
A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)填空: 31﹣30=2×3( ) ,
32﹣31=2×3( ) ,
33﹣32=2×3( ) ,
…
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;
(3)计算30+31+32+…+32016 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com