
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是; 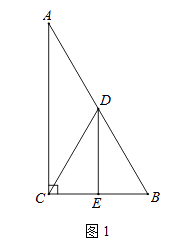
(2)如图2,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论; 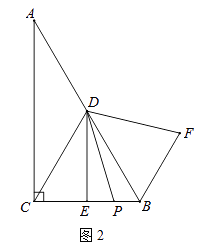
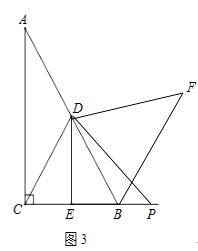
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系. 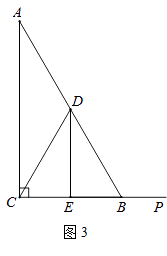
【答案】
(1)DE= ![]() ?BC
?BC
(2)解:BF+BP= ![]() DE.理由如下:
DE.理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
∴∠CDB﹣∠PDB=∠PDF﹣∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
 ,
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC﹣BP,
∴BF+BP=BC,
∵DE= ![]() BC,
BC,
∴BC= ![]() DE,
DE,
∴BF+BP= ![]() DE;
DE;
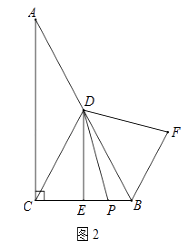
(3)解:如图,
与(2)一样可证明△DCP≌△DBF,
∴CP=BF,
而CP=BC+BP,
∴BF﹣BP=BC,
∴BF﹣BP= ![]() DE.
DE.
【解析】解:(1)∵∠ACB=90°,∠A=30°, ∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE= ![]() BC;
BC;
故答案为DE= ![]() BC.
BC.
(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,DE= ![]() BC;(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC﹣BP,DE=
BC;(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC﹣BP,DE= ![]() BC可得到BF+BP=
BC可得到BF+BP= ![]() DE;(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF﹣BP=BC,所以BF﹣BP=
DE;(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF﹣BP=BC,所以BF﹣BP= ![]() DE.
DE.


科目:初中数学 来源: 题型:
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
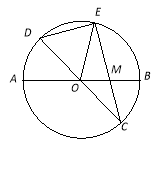
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=![]() .
.
(1)求证:![]() ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳的半径约为696000千米,用科学记数法可表示为( )
A.6.96×103千米
B.6.96×104千米
C.6.96×105千米
D.6.96×106千米
查看答案和解析>>
科目:初中数学 来源: 题型:
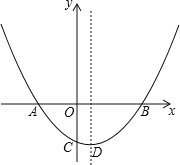
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)若点M为抛物线第四象限内一点,连接BC、CM、BM,求当△BCM的面积最大时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com