练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．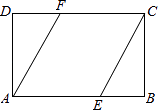

    【答案】证明：∵四边形ABCD是矩形， ∴DC∥AB，DC=AB，
    ∴CF∥AE，
    ∵DF=BE，
    ∴CF=AE，
    ∴四边形AFCE是平行四边形，
    ∴AF=CE．
    【解析】根据矩形的性质得出DC∥AB，DC=AB，求出CF=AE，CF∥AE，根据平行四边形的判定得出四边形AFCE是平行四边形，即可得出答案．
    【考点精析】关于本题考查的平行四边形的判定与性质和矩形的性质，需要了解若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积；矩形的四个角都是直角，矩形的对角线相等才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，某化工厂与A，B两地有公路和铁路相连，这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（吨千米），铁路运价为1.2元/（吨千米），这两次运输共支出公路运费15 000元，铁路运费97200元．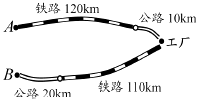
    （1）求化工厂从A地购买这批原料及利用这批原料生产的产品各多少吨？
    （2）计算这批产品的销售款比原料费和运输费的和多多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，点D是AB的中点，DE⊥BC，垂足为点E，连接CD．
    （1）如图1，DE与BC的数量关系是；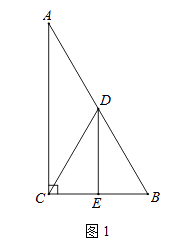
    （2）如图2，若P是线段CB上一动点（点P不与点B，C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论；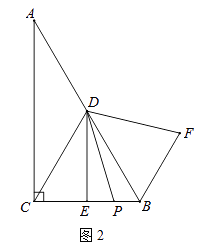
    （3）若点P是线段CB延长线上一动点，按照（2）中的作法，请在图3中补全图形，并直接写出DE、BF、BP三者之间的数量关系．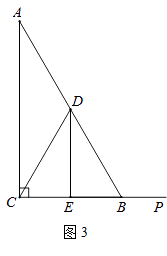

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当x＝－2时，多项式x2－kx＋4的值小于2，那么k的取值范围是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】给出下列各数：2，﹣3，﹣0.56，﹣11，35，0.618，﹣125，+2.5，﹣136，﹣2.333，0，其中负数有（　　）

    A. 4个 B. 5个 C. 6个 D. 7个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．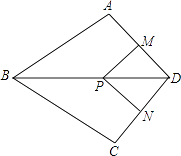
    （1）求证：∠ADB=∠CDB；
    （2）若∠ADC=90°，求证：四边形MPND是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB和CD相交于点O，∠DOE=90°，若∠BOE= ∠AOC．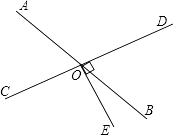
    （1）指出与∠BOD相等的角，并说明理由；
    （2）求∠BOD，∠AOD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】河流两岸a、b互相平行，C、D是河岸a上间隔50m的两个电线杆．某人在河岸b上的A处测得∠DAB=30°，然后沿河岸走了100m到达B处，测得∠CBF=60°，求河流的宽度CF的值（结果精确到个位）．

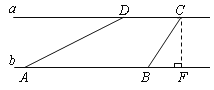
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠ABC+∠ECB=180°，∠P=∠Q，
    （1）AB与ED平行吗？为什么？
    （2）∠1与∠2是否相等？说说你的理由．

    查看答案和解析>>

    同步练习册答案